ユークリッド原論をどう読むか（１０）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第６巻

命題６ー１４（等積で等角な平行四辺形と逆比例）
（作図.直線図形の頂点共有と辺の１直線）
［平行四辺形の］完結
（１組の角が等しい平行四辺形と等角）
（作図.１組の角が等しい（よって等角な）平行四辺形）
等しくかつ等角な
　２つの平行四辺形の
　等しい角をはさむ辺は
　逆比例する。
そして
　等しい角をはさむ辺が
　逆比例する
　　等角な２つの平行四辺形は
　等しい。

• 等しいは、 公理１ー７ による。
• 等角は、 定義の補足（命題４ー２） による。
• 平行四辺形は、 定義の補足（命題１ー３４） による。
• 角は、 定義１ー８ による。
• 辺は、 定義１ー１９の補足 による。
• 逆比例は、 定義６ー２ による。

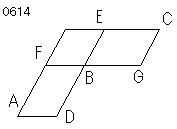
ＡＢ、ＢＣが
　等しくかつ等角 で、
　Ｂにおける角が
　等しい平行四辺形とし、
　ＤＢ、ＢＥが
　１直線をなすようにおかれたとせよ。

• 原論の立場は、
  　ずらしたり（平行な移動、回転による移動）、
  　ひっくりかえしたり（線対称による移動）して、
  　図形を適当な位置に移す
  　ことを認めている。
  この立場は、以下のように正当化される。
  　２つの直線図形Ａ、Ｂにおいて、
  　定義１ー１９の補足３（凸多角形）
  　公準１ー１（作図.直線）
  により、
  　Ａの任意の頂点Ｃ1.Ａから、
  　対角線をひいて、
  　順にできる三角形を、
  　Ｃ1Ｃ2Ｃ3、Ｃ1Ｃ3Ｃ4、…、Ｃ1Ｃn-1Ｃnとする。　
  　公準１ー２（作図.直線の延長）
  　命題１ー３の補足（作図.等しい線分となる点）
  により、
  　Ｂの任意の頂点Ｄ1.Ｂとその隣の頂点Ｄ2に対し
  　Ｅ2（延長Ｄ2Ｄ1；Ｄ1Ｅ2＝Ｃ1Ｃ2）
  をとり、
  　定義１ー１９の補足３（凸多角形）
  　命題１ー７の補足(作図.底辺に対する他の２辺の交点)
  により、
  　Ｄ1Ｄ2について、Ｂの他の頂点と異なる側に
  　Ｅ3（；Ｄ1Ｅ3＝Ｃ1Ｃ3、Ｅ2Ｅ3＝Ｃ2Ｃ3）
  をとると、
  　命題１ー８の補足（３辺相等による合同）
  により、
  　△Ｃ1Ｃ2Ｃ3≡△Ｄ1Ｅ2Ｅ3
  となる。
  　同様に、
  　Ｄ1Ｄ2について、Ｂの他の頂点と異なる側に
  　Ｅ4（；Ｄ1Ｅ4＝Ｃ1Ｃ4、Ｅ3Ｅ4＝Ｃ3Ｃ4）
  をとると、
  　命題１ー８の補足（３辺相等による合同）
  により、
  　△Ｃ1Ｃ3Ｃ4≡△Ｄ1Ｅ3Ｅ4
  となる。
  以下、順に繰り返しすと、
  　△Ｃ1Ｃn-1Ｃn≡△Ｄ1Ｅn-1Ｅn
  となり、
  　図形Ｄ1Ｅ2…Ｅn≡Ａ
  となる。
  よって、
  　どのような直線図形でも、
  　図形の内部は重ならずに、
  　それぞれの任意の１頂点を共有し、
  　その頂点をつくる１辺を
  　１直線となるように移動することができる。
  （以下、命題６−１４の補足 （作図.直線図形の頂点共有と辺の１直線）という。）
  　
• 　２つの平行四辺形において、１組の角が等しければ、等角である。
  （以下、命題６−１４の補足３ （１組の角が等しい平行四辺形と等角）という。）
  平行四辺形ＡＤＢＦとＣＧＢＥにおいて、
  　∠ＤＢＦ＝∠ＧＢＥ
  ならば、
  　命題１ー２９（平行と錯角、内対角、同側内角）
  により、
  　∠ＤＢＦ＋∠ＢＤＡ
  　＝∠ＧＢＥ＋∠ＢＧＣ＝∠Ｒ、
  　公理１ー３（等しいものから等しいものをひく）
  により
  　∠ＢＤＡ＝∠ＢＧＣ。
  また、
  　命題１ー３４（平行四辺形の対辺・対角・対角線）
  により
  　∠ＤＢＦ＝∠ＦＡＤ、
  　∠ＧＢＥ＝∠ＥＣＧ
  となり
  　∠ＤＢＦ＝∠ＧＢＥ
  となっているから、
  　公理１ー１の補足（等しいものに等しい）
  により
  　∠ＦＡＤ＝∠ＥＣＧ。
  同様にして、
  　∠ＡＤＢ＝∠ＣＧＢ。
  したがって、
  　平四ＡＤＢＦ;(等角)平四ＣＧＢＥ
  となる。
• １組の角が等しい（よって等角な）平行四辺形を作図すること。
  （以下、命題６ー１４の補足４（作図.１組の角が等しい（よって等角な）平行四辺形）という。） 作図の方法は次のとおり。
  平行四辺形ＡＢと線分ＢＥ、ＢＧ’があるとき、
  　命題１ー２３（作図・直線上に指定された角）
  により、
  　半直線ＢＧ"(;;∠ＥＢＧ”＝∠ＤＢＦ,同向側(ＥＢ,ＤＢ,Ｆ))を引き、
  　命題１ー３の補足（作図.等しい線分となる点）
  により
  　Ｇ(ＢＧ";;ＢＧ＝ＢＧ')
  をとる。
  命題１ー３１（作図・平行線）
  により
  　平行線ＥＣ'(Ｅ,ＢＧ)、
  　平行線ＧＣ"(Ｇ,ＢＥ)
  をひく。
  　命題１ー３０の補足(交線に平行な線)
  により、
  　交点Ｃ(ＥＣ',ＧＣ")
  をとる。
  定義の補足（命題１ー３４）(平行四辺形・対角線)
  により、
  　ＢＥＣＧは平行四辺形である。　
  
• 　本命題の前半においては、
  　平行四辺形ＡＢ
  に対して、
  　等しい平行四辺形を
  　まえもって作図すること
  を前提としていない。
  　仮想的に作図できたとして
  　推論を進めている。
  本命題の後半により、
  　等しい平行四辺形が
  　実際的に作図できる
  ことになる。
  
• 　平行四辺形ＢＥＣＧ(ＢＥ,ＢＧ
  　　;;Ｇ;上.延長ＦＢ,∠ＦＢＤ＝∠ＥＢＧ
  　　,平四ＢＥＣＧ＝平四ＡＦＢＤ)
  をとっている。

そうすれば
　ＦＢ、ＢＧも１直線をなす。

• ＤＢ、ＢＥが１直線となっているから、
  　角ＦＢＤと角ＥＢＦの和は２直角である。
  角ＥＢＧと角ＦＢＧが
  　命題の設定により等しいので、
  　公理１ー２（等しいものに等しいものを加える）
  により、
  　角ＥＢＧと角ＥＢＦの和も２直角である。
  したがって、
  　命題１ー１４（直線と２直角２）
  により、ＦＢ、ＢＧが１直線をなす。
• 　Ｇ;上.ＦＢ
  となっている。

ＡＢ、ＢＣの等しい角をはさむ辺は
　逆比例する。
すなわち
　ＤＢがＢＥに対するように、
　ＧＢがＢＦに対する
　と主張する。
　
平行四辺形ＦＥが完結されたとせよ。

• ［平行四辺形の］完結とは、
  　作図を完成するさせることである。
  （以下、コメント２（命題６ー１４）(［平行四辺形の］完結)という。）
  　公準１ー２（作図.直線の延長）
  により
  　延長ＡＦ、延長ＥＣ
  をとる。
  　ＡＦ(交)ＢＧ、
  　命題１ー３０の補足(交線に平行な線)
  により、
  　交点Ｈ(延長ＡＦ,延長ＥＣ)
  をとると、
  　命題の設定により、
  　ＦＢ‖ＨＥ、ＢＥ‖ＦＨ
  だから、
  　定義の補足（命題１ー３４）(平行四辺形・対角線)
  により、
  　ＨＦＢＥ;平行四辺形
  となる。
  
• 　平四ＦＥ
  となっている。

そうすれば
　平行四辺形ＡＢは
　平行四辺形ＢＣに等しく、

• 　平四ＡＢ＝平四ＢＣ
  となっている。

　ＦＥは別の平行四辺形であるから、
　ＡＢがＦＥに対するように、
　ＢＣがＦＥに対する。

• 命題５ー７（同一量の比）
  による。
• 　平四ＡＢ：平四ＦＥ＝平四ＢＣ：平四ＦＥ
  となっている。

ところが
　ＡＢがＦＥに対するように
　ＤＢがＢＥに対し、
　ＢＣがＦＥに対するように、
　ＧＢがＢＦに対する。

• 命題６ー１（同高の三角形、平行四辺形は底辺と比例）
  による。
• 　平四ＡＢ：平四ＦＥ＝ＤＢ：ＢＥ、
  　平四ＢＣ：平四ＦＥ＝ＧＢ：ＢＦ
  となっている。

それゆえ
　ＤＢがＢＥに対するように、
　ＧＢがＢＦに対する。

• 命題５ー１１（同一の比に同じ比）
  による。
• 　ＤＢ：ＢＥ＝ＧＢ：ＢＦ
  となっている。

ゆえに
　平行四辺形ＡＢ、ＢＣの
　　等しい角をはさむ辺は
　逆比例する。

• 定義６ー２（三角形の辺の平行線による辺の比例区分）
  による。

次に
　ＤＢがＢＥに対するように、
　ＧＢがＢＦに対するとせよ。

• 等しい角Ｂをはさむ辺が逆比例する
  　等角な２つの平行四辺形ＡＢ、ＢＣを
  　命題６−１４の補足（作図.直線図形の頂点共有と辺の１直線）
  により、
  　ＤＢ、ＢＥが１直線となるようにすると、
  　前半と同じように、
  　公準１ー２（作図.直線の延長）、
  　命題１ー３０の補足(交線に平行な線)、
  　定義の補足（命題１ー３４）(平行四辺形・対角線)
  により、
  　平行四辺形ＦＥが完結する。
  
• 　本命題の後半においては、
  　作図が可能であり、
  　実際的である。
• 　平行四辺形ＡＤＢＦと線分ＢＥ'
  に対して、
  　Ｅ(延長ＤＢ;;ＢＥ＝ＢＥ')、
  　Ｇ(延長ＦＢ;;ＤＢ：ＢＥ＝ＧＢ：ＢＥ)、
  　平四ＢＧＣＥ(ＢＧ,ＢＥ)、
  　平四(ＢＥ,ＢＦ)
  をとっている。

平行四辺形ＡＢは
　平行四辺形ＢＣに等しい
　と主張する。
ＤＢがＢＥに対するように、
　ＧＢがＢＦに対し、

• 命題の設定 による。
• 　ＤＢ：ＢＥ＝ＧＢ：ＢＦ
  となっている。

　他方
　ＤＢがＢＥに対するように、
　平行四辺形ＡＢが平行四辺形ＦＥに対し、
　ＧＢがＢＦに対するように
　平行四辺形ＢＣが平行四辺形ＦＥに対する

• 　ＤＢ：ＢＥ＝平四ＡＢ：平四ＦＥ、
  　ＧＢ：ＢＦ＝平四ＢＣ：平四ＦＥ
  となっている。

から、
　ＡＢがＦＥに対するように、
　ＢＣがＦＥに対する。

• 命題６ー１（同高の三角形、平行四辺形は底辺と比例）、
  命題５ー１１（同一の比に同じ比）
  による。
• 　平四ＡＢ：平四ＦＥ＝平四ＢＣ：平四ＦＥ
  となっている。

それゆえ
　平行四辺形ＡＢは
　平行四辺形ＢＣに等しい。

• 命題５ー９（同一比の量）
  による。
• 　平四ＡＢ＝平四ＢＣ
  となっている。

よって
　等しくかつ等角 な２つの平行四辺形の
　等しい角をはさむ辺は
　逆比例する。
そして
　等しい角をはさむ辺が逆比例する
　等角 な２つの平行四辺形は
　等しい。
これが証明すべきことであった。

• 命題６ー１４は、
  　平四(ＤＢ,ＢＦ)、平四(ＧＢ,ＢＥ)
  　∠ＤＢＦ＝∠ＧＢＥ
  に対して、
  　平四(ＤＢ,ＢＦ)＝平四(ＧＢ,ＢＥ)
  ならば
  　ＤＢ：ＢＥ＝ＧＢ：ＢＦ、
  逆に、
  　ＤＢ：ＢＥ＝ＧＢ：ＢＦ
  ならば
  　平四(ＤＢ,ＢＦ)＝平四(ＧＢ,ＢＥ)
  のことである。
• 命題６−１４の補足 （作図.直線図形の頂点共有と辺の１直線）

  前提	作図	推論
  定義		1-19補3
  公準	1-1,1-2
  公理
  命題	1-3補,1-7補	1-8補
  その他

• 命題６−１４の補足３ （１組の角が等しい平行四辺形と等角）

  前提	作図	推論
  定義
  公準
  公理		1-1補,1-3
  命題		1-29,1-34
  その他

• 命題６ー１４の補足４（作図.１組の角が等しい（よって等角な）平行四辺形）

  前提	作図	推論
  定義		補(題1-34)
  公準
  公理
  命題	1-3補,1-23,1-31	1-30補
  その他

• 命題６ー１４は推論用命題である。

  前提	作図	推論
  定義		補(題1-34),6-2
  公準	1-2
  公理		1-1補,1-2
  命題	1-30補,6-14補	1-14,5-7,5-9,5-11,6-1
  その他	平行四辺形の完結

前 　　 次 　　 目次 　　頁頭