ユークリッド原論をどう読むか（８）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第４巻

命題４ー２（作図.等角三角形の内接）
等角

与えられた円に
　与えられた三角形に等角な三角形を
　内接させること。

• 円は、 定義１ー１５ による。
• 三角形は、 定義１ー１９の補足２ による。
• 等角は、
  　対応する角が
  　すべて等しいということである。
  （以下、定義の補足（命題４ー２）(等角)という。）
  三角形について言えば
  　相似であるが、
  　原論においては
  相似は、
  　円の切片以外には登場していない。
  四角形では、
  　必ずしも相似とはならない。
  すべての長方形は等角であるが、
  　すべてが相似とはならない。
• 内接は、 定義４ー３ による。

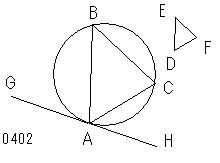
与えられた円をＡＢＣ、
　与えられた三角形をＤＥＦとせよ。

• 　円ＡＢＣ、
  　△ＤＥＦ
  をとっている。

このとき
　円ＡＢＣに
　三角形ＤＥＦに等角な三角形を
　内接させねばならぬ。

円ＡＢＣに
　Ａで接するＧＨがひかれ、

• 命題３ー１６の補足３ （円周上の点を通る接線）
  による。
• 　点Ａ[円ＡＢＣ]、
  　垂線ＡＧ(Ａ,直径(Ａ,円ＡＢＣ))]、
  　点Ｈ[延長ＡＧ]
  をとれば、
  　ＧＨ（接）円ＡＢＣ
  となっている。

　直線ＡＨ上に
　その上の点Ａにおいて
　角ＤＥＦに等しい角ＨＡＣが、 【・・・(a)】

• 命題１ー２３ （作図・直線上に指定された角）
  により、
  　直線ＡＨについて
  　円と同じ側に
  　角ＨＡＣをつくる。
  命題３ー１６ （直径に直角な直線）
  により
  直線ＡＣは
  　円の内部に入る。
  命題３−２の補足 (円内通過直線は円周と２交点)
  により、
  直線ＡＣは
  　Ａ以外に
  　もう１点で円周と交わる。
  その点を改めてＣとし、
  　Ｃを溯って用いている。
• 　∠ＨＡＺ(Ａ,ＡＨ,∠ＤＥＦ,同側(ＧＨ,円ＡＢＣ))、
  　交点Ｃ(ＡＺ,円ＡＢＣ;;外.Ａ)
  をとっている。

　直線ＡＧ上に
　その上の点Ａにおいて
　角ＤＦＥに等しい角ＧＡＢが
　つくられたとし、

• 命題１ー２３ （作図・直線上に指定された角）
  による。
  　Ｂが円周上にとれるのは
  　Ｃと同じ理由による。
• 　∠ＧＡＹ(Ａ,ＡＧ,∠ＤＦＥ,同側(ＧＨ,Ｃ))、
  　交点Ｂ(ＡＹ,円ＡＢＣ;;外.Ａ)
  をとっている。

　ＢＣが結ばれたとせよ。

• 公準１ー１ （作図.直線）
  による。
• 　線分ＢＣ
  をとっている。

そうすれば
直線ＡＨは
　円ＡＢＣに接し、

• (a) による。
• 　ＡＨ（接）円ＡＢＣ
  となっている。

　接点Ａから
　円に弦ＡＣがひかれたから、

• (a) による。
• 　ＡＣ;弦.円ＡＢＣ
  となっている。

角ＨＡＣは
　円の
　反対側の切片内の角ＡＢＣに等しい。

• 命題３ー３２ （いわゆる接弦定理）
  による。
• 　∠ＨＡＣ＝∠ＡＢＣ
  となっている。

ところが
角ＨＡＣは
　角ＤＥＦに等しい。

• (a) による。
• 　∠ＨＡＣ＝∠ＤＥＦ
  となっている。

それゆえ
角ＡＢＣも
　角ＤＥＦに等しい。

• 公理１ー１ （同じものに等しい）
  による。
• 　∠ＡＢＣ＝∠ＤＥＦ
  となっている。

同じ理由で
角ＡＣＢも
　角ＤＦＥに等しい。

• 　∠ＡＣＢ＝∠ＤＦＥ
  となっている。

ゆえに
残りの角ＢＡＣも
　残りの角ＥＤＦに等しい。

• 命題１ー３２ （三角形の内対角・内角の和）
  による。
• 　∠ＢＡＣ＝∠ＥＤＦ
  となっている。

よって
　与えられた円に
　与えられた三角形に等角な三角形が
　内接された。
これが作図すべきものであった。
　

• 命題４ー２は、
  　円ＡＢＣ、
  　△ＤＥＦ
  に対して、
  　接線ＧＨ(点Ａ[円周ＡＢＣ],円ＡＢＣ)、
  　弦ＡＣ..円ＡＢＣ(Ａ,点Ｃ(円周ＡＢＣ;∠ＨＡＣ＝∠ＤＥＦ)))、
  　弦ＡＢ..円ＡＢＣ(Ａ,点Ｂ(円周ＡＢＣ;∠ＧＡＢ＝∠ＤＦＥ)))、
  　弦ＢＣ..円ＡＢＣ(Ｂ,Ｃ)
  をとれば、
  　△ＡＢＣ;（等角）△ＤＥＦ、
  　△ＡＢＣ;（内接）円ＡＢＣ
  のことである。
  
• 命題４ー２は作図用命題である。

  前提	作図	推論
  定義
  公準	1-1
  公理		1-1
  命題	1-23,3-2補,3-16補3	1-32,3-16,3-32
  その他

前 　　 次 　　 目次 　　頁頭