ユークリッド原論をどう読むか（２）
頁末 　　 前 　　 次 　　 目次　

ユークリッド原論
第１巻

命題１ー２３（作図・直線上に指定された角）
与えられた直線上に
　その上の点において
　与えられた直線角に等しい直線角をつくること。

• 直線は、定義１ー４による。
• 点は、定義１ー１による。
• 直線角は、定義１ー９による。
• 等しいは、公理１ー７による。

与えられた直線をＡＢ、
　その上の点をＡ、
　与えられた直線角を角ＤＣＥ
とせよ。

• 　直線ＡＢ、
  　∠ＤＣＥ
  をとっている。

このとき
　与えられた直線ＡＢ上に
　その上の点Ａにおいて
　与えられた直線角ＤＣＥに
　等しい直線角をつくらねばならぬ。

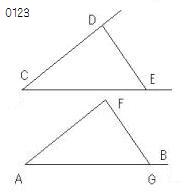
ＣＤ、ＣＥの双方の上に
　任意の点Ｄ、Ｅがとられ、

• 公準１ー１の補足（作図.任意の点をとる）
  による。

ＤＥが結ばれたとせよ。

• 公準１ー１（作図.直線）
  による。
• 　線分(Ｄ,Ｅ)
  をとっている。

そして
　３線分ＣＤ、ＤＥ、ＣＥに
　等しい３線分から
　三角形ＡＦＧがつくられ、
　ＣＤはＡＦに、ＣＥはＡＧに、ＤＥはＦＧに
　等しくなるようにせよ。
　　　　　　【・・・(a)】

• 　命題１ー３の補足（作図.等しい線分となる点）
  により、
  　ＡＢ上に
  　ＡＧがＣＥに等しくなるようにＧをとり、
  　ＡＦがＣＤに、
  　ＦＧがＤＥに等しくなるように
  　命題１ー２２作図・３線分から三角形）
  により三角形をつくる。
  
• この３線分は、
  　三角形をつくっていたものであるから、
  　命題１ー２０（三角形の２辺の和と１辺）
  により、
  　命題１ー２２（作図・３線分から三角形）
  の条件を満たす。
• 　点Ｇ(半直ＡＢ;;ＡＧ＝ＡＥ)、
  　点Ｆ;頂点.三角(_ＡＧ;;ＡＦ＝ＣＤ,ＧＦ＝ＥＤ)
  をとっている。

そうすれば
　２辺ＤＣ、ＣＥは
　２辺ＦＡ、ＡＧにそれぞれ等しく、
　底辺ＤＥは底辺ＦＧに等しいから、
　角ＤＣＥは角ＦＡＧに等しい。

• 　(a) ,
  　命題１ー８（３辺相等２）
  による。
• 　(ＤＣ,ＣＥ)＝(ＦＡ,ＡＧ)、
  　ＤＥ＝ＦＧ
  　∠ＤＣＥ＝∠ＦＡＧ
  となっている。

よって
　与えられた直線ＡＢ上に
　その上の点Ａにおいて
　与えられた直線角ＤＣＥに
　等しい直線角ＦＡＧがつくられた。

• 　前節による。

これが作図すべきものであった。

• 　命題1-23は
  　直線ＡＢ、
  　∠ＤＣＥ
  に対して、
  　点Ｇ(半直ＡＢ;;ＡＧ＝ＡＥ)、
  　点Ｆ;頂点.三角(_ＡＧ;;ＡＦ＝ＣＤ,ＧＦ＝ＥＤ)
  をとれば、
  　∠ＤＣＥ＝∠ＦＡＧ
  のことである。
• 　命題1-23は作図用命題である。
  

  前提	作図	推論
  定義
  公準	1-1,1-1補
  公理
  命題	1-3補,1-22	1-8、1-20
  その他

今回は、ここで紙面が尽きてしまった。
前号と併せて既にお気づきと思われるが、
　原論の命題は
　「これが作図すべきものであった。」か
　「これが証明すべきことであった。」で証明が終わる。
このことからわかるとおり、
　命題は、作図用のものと推論用のものとに分類できる。
　この観点に立てば、
　公準や公理も作図用と推論用に
　分かれるのではないかと考えて、
　各命題のコメントの最後に
　表としてまとめてある。
まとめから判断するに、
　前号の最初に指摘したことだが、
　公準は作図に関係し、
　公理は推論に関係していることが間違いない。
　この論考の目的の一つは、
　このことの実証である。
どこまで実証できるか心もとないが、
　せめて第一巻を終えることを目標としたい。

前 　　 次 　　 目次 　　頁頭