ユークリッド原論をどう読むか（１）
頁末 　　 前 　　 次 　　 目次　

ユークリッド原論
第１巻

命題１ー７（３辺相等１）　
(作図.底辺に対する他の２辺の交点)
　一つの線分を底辺
として、
　［それと］三角形をなす２線分に
　それぞれ等しく、
　同じ側にことなった点で交わり、
　最初の２線分と同じ端をもつ
［ような］
　他の２線分をつくることはできない。

• 　線分は定義の補足（命題１ー１）による。
• 　底辺は定義１ー２０の補足２による。
• 　三角形は定義１ー１９の補足２による。
• 　等しいは公理１ー７による。
• 　同じ側は定義１ー７の補足による。
• 　点は定義１ー３による。
• 　交わるは定義１ー８の補足による。
• 　三角形があって、
  　底辺と考える１辺以外の
  　２辺（２線分）について
  　考察している。
• 　この命題は
  　次のように表現することができる。
  「一つの線分を底辺として
  　三角形をなす２線分は、
  　それぞれ
  　その底辺に等しい線分と対応する端を共有し、
  　かつ、
  　その線分について同じ側において、
  　互いに他の端として共有しうる点を
  　ただ１つとることができる。」
  こうすると、
  　作図用命題とみなせる。
  　（以下、命題１ー７の補足(作図.底辺に対する他の２辺の交点)という。）

もし可能ならば、

• 背理法の仮定である。
• 　作図としては、
  　実際は不可能であるが、
  　敢えて可能であるとして
  　推論を進める
  という意味である。
  （以下、コメント２(命題１−７） (もし可能ならば)という。）

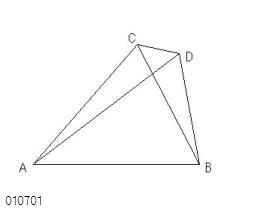
　同一の線分ＡＢ上に点Ｃで交わる
　２線分ＡＣ、ＣＢ
が与えられ、

• 　線分(Ａ,Ｂ)、
  　Ｃ;点(ＡＢ外)、
  　線分(Ａ,Ｃ)、
  　線分(Ｃ,Ｂ)
  をとっている。　

　それとそれぞれ等しく同じ側に
　ことなった点Ｄで交わり
　同じ端をもつ
　他の２線分ＡＤ、ＤＢ
がつくられ、
　ＣＡはＤＡに等しく同じ端Ａをもち、
　ＣＢはＤＢに等しく同じ端をもつ
ようにされ、

• 　Ｄ;点(Ｃ外、ＡＢについてＣと同じ側)、
  　線分(Ａ,Ｄ)＝ＡＣ、
  　線分(Ｄ,Ｂ)＝ＣＢ、
  をとっている。
  

　ＣＤが結ばれた
とせよ。

• 公準１ー1（作図.直線）
  による。
• 　線分(Ｃ,Ｄ)
  をとっている。
• 　Ｄの位置が、
  　線分ＡＣについて
  　Ｂと同じ側か反対側か
  と同時に、
  　線分ＢＣについて
  　Ａと同じ側か反対側か
  の４通りがある。
  　Ｄが、
  　線分ＡＣについてＢと同じ側で、
  　線分ＢＣについてＡと反対側である
  ことと、
  　Ｄが、
  　線分ＡＣについてＢと反対側で、
  　線分ＢＣについてＡと同じ側である
  ことは、
  　ＣとＤの記号を付け替えれば同じであり、
  　Ｄが、
  　線分ＡＣについてＢと同じ側で、
  　線分ＢＣについてＡと同じ側である
  ことと、
  　Ｄが、
  　線分ＡＣについてＢと反対側で、
  　線分ＢＣについてＡと反対側である
  ことも、
  　ＣとＤの記号を付け替えれば同じである
  から、
  　Ｄが、
  　線分ＡＣについてＢと同じ側で、
  　線分ＢＣについてＡと反対側である
  場合と、
  　Ｄが、
  　線分ＡＣについてＢと同じ側で、
  　線分ＢＣについてＡと同じ側である
  場合とを論証すればよい。
  そこで、
  　Ｄについて
  　線分ＡＣでＢと同じ、線分ＢＣでＡと反対になる場合
  　線分ＡＣでＢと同じ、線分ＢＣでＡと同じになる場合
  　に場合分けする。
  
  　この図は、
  　線分ＡＣでＢと同じ、線分ＢＣでＡと反対
  になる場合である。

そうすれば、
　[線分ＡＣでＢと同じ、
　線分ＢＣでＡと反対になる場合]
　ＡＣはＡＤに等しい
から、

• 　命題の設定 による。
• 　ＡＣ＝ＡＤ
  となっている。

　角ＡＣＤも角ＡＤＣに等しい。

• 　前節、
  　命題１ー5（２等辺三角形の底角）
  による。
• 　∠ＡＣＤ＝∠ＡＤＣ
  となっている。

それゆえ
　角ＡＤＣは角ＤＣＢより大きい。

• 　角ＡＣＤは角ＤＣＢより大きく、
  　角ＡＤＣは角ＡＣＤに等しい
  ので、
  　公理１ー８の補足２（等より大・小、大・小に等）
  による。
• 　∠ＡＤＣ＞∠ＤＣＢ
  となっている。

したがって
　なおさら
　角ＣＤＢは角ＤＣＢより大きい
　　　　　　【・・・(1)】 。

• 角ＣＤＢは角ＡＤＣより大きく、
  　角ＡＤＣは角ＤＣＢより大きいので、
  　公理１ー８の補足３（大きい・小さいものより大きい・小さい）
  による。
• 　∠ＣＤＢ＞∠ＤＣＢ
  となっている。

また、
　ＣＢはＤＢに等しい

• 命題の仮説 による。
• 　ＣＢ＝ＤＢ
  となっている。

から
　角ＣＤＢも角ＤＣＢに等しい。

• 　前節、
  　命題１ー5（２等辺三角形の底角）
  による。
• 　∠ＣＤＢ＝∠ＤＣＢ
  となっている。

ところが、
　それよりなおさら大きいことも証明された。

• 　(1) による。
• 　∠ＣＤＢ＞∠ＤＣＢ
  となっている。

　これは不可能である。

• 背理法による。
• 以下、
  　線分ＡＣでＢと同じ、
  　線分ＢＣでＡと同じになる場合
  
  
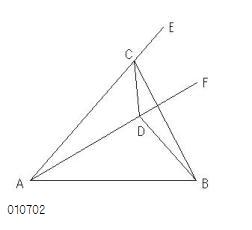
  　ＡＣはＡＤに等しい
  
  • 命題の仮定 による。
  • 　ＡＣ＝ＡＤ
    となっている。
  から、
  　角ＥＣＤも角ＦＤＣに等しい。
  • 命題１ー5（２等辺三角形の底角）
    による。
  • 　∠ＥＣＤ＝∠ＦＤＣ
    となっている。
  それゆえ
  　角ＦＤＣは角ＢＣＤより大きい。
  • 　角ＥＣＤは角ＢＣＤより大きく、
    　角ＦＤＣは角ＥＣＤに等しい
    ので、
    　公理１ー８の補足２（等より大・小、大・小に等）
    による。
  • 　∠ＦＤＣ＞∠ＢＣＤ
    となっている。
  したがって
  　なおさら
  　角ＢＤＣは角ＢＣＤより大きい
  　　　　　　【・・・(2)】 。
  • 
    　角ＢＤＣは角ＦＤＣより大きく、
    　角ＦＤＣは角ＢＣＤより大きい
    ので、
    　公理１ー８の補足３（大きい・小さいものより大きい・小さい）
    による。
  • 　∠ＢＤＣ＞∠ＢＣＤ
    となっている。
  また、
  　ＣＢはＤＢに等しい
  
  • 命題の仮説による。
  • 　ＣＢ＝ＤＢ
    となっている。
  から
  　角ＢＤＣも角ＢＣＤに等しい。
  • 　前節、
    　命題１ー5（２等辺三角形の底角）
    による。
  • 　∠ＢＤＣ＝∠ＢＣＤ
    となっている。
  ところが、
  　それよりなおさら大きいことも証明された。
  
  • 　(2) による。
  • 　∠ＢＤＣ＞∠ＢＣＤ
    となっている。
  　これは不可能である。
  • 　背理法による。

［ したがって、
　２つの場合の結果から
　不可能であるとわかる。］

〔よって〕
　一つの線分を底辺
として、
　三角形をなす２線分にそれぞれ等しく、
　同じ側にことなった点で交わり、
　最初の２線分と同じ端をもつ
　他の２線分をつくる
ことはできない。

• 他の命題のスタイルと合わせるとすると、
  　〔よって〕が必要であろう。

　これが証明すべきことであった。

• 　命題１ー７の証明に
  　ギャップがある
  ことは
  　これまでも指摘されてきた。
  　命題１ー５（２等辺三角形の底角）
  の中に、
  　二等辺三角形の底角が等しいことの証明において、
  　底辺の下の角に注目している
  ことを考慮すると、
  　ユークリッドも分かっていた
  　が、
  　命題１ー７をきちんと訂正せずに
  　きてしまった
  のではないかと思われた。
  ところが、
  　「ユークリッド『原論』とは何か（斎藤 憲）」
  によれば、
  　すべての場合を尽くさずに
  　１つの場合のみ証明するのが
  　原論のスタイルである
  ということである。
  　なるほどそうかとも思われる。
• 命題1-7は、
  　△ＡＢＣ
  に対し、
  　Ｄ；線分ＡＤ＝ＡＣ、
  　　　線分ＢＤ＝ＢＣ、
  　　　ＡＢについてＣと同じ側
  ならば、
  　Ｄ≡Ｃ
  のことである。
  
• 命題１ー７の補足(作図.底辺に対する他の２辺の交点)

  前提	作図	推論
  定義
  公準
  公理
  命題		1-7
  その他

• 命題1-7は推論用命題である。

  前提	作図	推論
  定義
  公準	1-1
  公理		1-8補2,1-8補3
  命題		1-5
  その他		背理法,コ2(題1-7),場合わけ

前 　　 次 　　 目次 　　頁頭