ユークリッド原論をどう読むか（９511）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第５巻

命題５ー１１（同一の比に同じ比）
（同じ比は互いに同じ）
（等しい量は同じ比をもつ）
対する・ように


同一の比に同じ比は
　互いに同じである。

• 比は、定義５ー３ による。
• 同じ比は、定義５ー５ による。

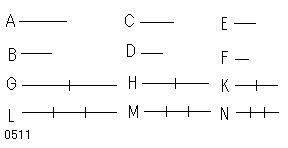
ＡがＢに対するように、
　ＣがＤに対し、
　ＣがＤに対するように、
　ＥがＦに対するとせよ。

• 　ＡがＢに対する
  とは、
  　ＡがＢに、
  　ある比でもって対している
  ということである。
  　ＡがＢに対するように
  　ＣがＤに対する
  とは、
  　ＡがＢに対している比と
  　ＣがＤに対している比が
  　同じである
  ということである。
  以下、定義の補足３（命題５ー１１）(対する・ように)という。
• 　Ａ：Ｂ＝Ｃ：Ｄ
  　Ｃ：Ｄ＝Ｅ：Ｆ
  となっている。

ＡがＢに対するように、
　ＥがＦに対すると主張する。
　

• 同じ比をもつ線分の作図（仮想的）は
  コメント２（命題５ー４）参照のこと。

Ａ、Ｃ、Ｅの［任意の］同数倍Ｇ、Ｈ、Ｋと、
　Ｂ、Ｄ、Ｆの別の任意の同数倍Ｌ、Ｍ、Ｎが
　とられたとせよ。【・・・(a)】

• 推論の設定である。
• 量の倍は、命題の補足（定義５ー２）（作図.倍量）
  による。
• 「［任意の］同数倍 」については、
  　コメント（命題５ー４） を参照のこと。
• 　(Ｇ、Ｈ、Ｋ)＝ｍ(Ａ、Ｃ、Ｅ)、
  　(Ｂ、Ｄ、Ｆ)＝ｎ(Ｌ、Ｍ、Ｎ)
  をとっている。

そうすれば
　ＡがＢに対するように
　ＣがＤに対し、

• 命題の設定による。
• 　Ａ：Ｂ＝Ｃ：Ｄ
  となっている。

　そして
　Ａ、Ｃの［任意の］同数倍Ｇ、Ｈと
　Ｂ、Ｄの別の任意の同数倍Ｌ、Ｍとが
　とられたから、

• (a) による。
• 　(Ｇ、Ｈ)＝ｍ(Ａ、Ｃ)、
  　(Ｌ、Ｍ)＝ｎ(Ｂ、Ｄ)
  となっている。

　もし
　ＧがＬより大きければ、
　ＨもＭより大きく、
　等しければ、等しく、
　小さければ小さい。 【・・・(1)】

• 定義５ー５（同じ比）
  による。
• 　Ｇ(＜、＝、＞)Ｌ
  ならば、
  　Ｈ(＜、＝、＞)Ｍ
  となっている。

また
　ＣがＤに対するように、
　ＥがＦに対し、

• 命題の設定による。
• 　Ｃ：Ｄ＝Ｅ：Ｆ
  となっている。

　そして
　Ｃ、Ｅの［任意の］同数倍Ｈ、Ｋと
　Ｄ、Ｆの別の任意の同数倍Ｍ、Ｎとが
　とられたから、

• (a) による。
• 　(Ｈ、Ｋ)＝ｍ(Ｃ、Ｅ)、
  　(Ｍ、Ｎ)＝ｎ(Ｄ、Ｆ)
  となっている。

　もし
　ＨがＭより大きければ、
　ＫもＮより大きく、
　等しければ、等しく、
　小さければ、小さい。 【・・・(2)】

• 定義５ー５（同じ比）
  による。
• 　Ｈ(＜、＝、＞)Ｍ
  ならば、
  　Ｋ(＜、＝、＞)Ｎ
  となっている。

《 ところがもし
　ＨがＭより大きければ
　ＧもＬより大きく、
　等しければ、等しく、
　小さければ、小さかった。

• 推論の流れを、
  　この１節が混乱させている。
  すなわち、
  「ＡならばＢ。
  　ＢならばＣ。
  よって
  　ＡならばＣ。」
  が推論の筋道である。
  しかし、
  　原論のここでの推論は、
  「ＢならばＡ。
  　ＢならばＣ。
  　よってＡならばＣ。」
  となっている。
• ここまでの推論では、
  　Ｇ(＜、＝、＞)Ｌ
  ならば、
  　Ｈ(＜、＝、＞)Ｍ
  となっている。

それゆえもし》［したがって］
　ＧがＬより大きければ、
　［ＨもＭより大きいので］
　ＫもＮより大きく、
　等しければ、等しく、
　小さければ、小さい。

• (1)(2)による。
  
• 　Ｇ(＜、＝、＞)Ｌ
  ならば、
  　Ｋ(＜、＝、＞)Ｎ
  となっている。

そして
　Ｇ、ＫはＡ、Ｅの［任意の］同数倍であり、
　Ｌ、ＮはＢ、Ｆの別の任意の同数倍である。

• (a) による。
• 　(Ｇ、Ｋ)＝ｍ(Ａ、Ｅ)、
  　(Ｌ、Ｎ)＝ｎ(Ｂ、Ｆ)
  

ゆえに
　ＡがＢに対するように、
　ＥがＦに対する。

• 定義５ー５（同じ比）
  による。

よって
　同一の比に同じ比は互いに同じである。

• 「互いに」という部分の論証が、
  　原論では欠いている。
  
• この論証は定義５ー５（同じ比）
  を少し補足した
  　次の命題５ー１１の補足（同じ比は互いに同じ）
  による。
  すなわち、
  「ＡがＢに対するように、
  　ＣがＤに対するなら、
  　ＣがＤに対するように、
  　ＡがＢに対する。」
  （以下、命題５ー１１の補足（同じ比は互いに同じ）という。）
  これは、次のように証明される。
  ＡがＢに対するように、
  　ＣがＤに対するので、
  
  • 　Ａ：Ｂ＝Ｃ：Ｄ
    となっている。
  
  　定義５ー５（同じ比）
  により、
  　Ａ、Ｃの［任意の］同数倍Ｇ、Ｈと、
  　Ｂ、Ｄの別の任意の同数倍Ｌ、Ｍが
  　とられたとすると、
  
  • 　(Ｇ、Ｈ)＝ｍ(Ａ、Ｃ)、
    　(Ｌ、Ｍ)＝ｎ(Ｂ、Ｄ)
    をとっている。
  
  　ＧがＬより大きければ、
  　ＨもＭより大きく、
  　等しければ、等しく、
  　小さければ小さい。
  
  • 　Ｇ(＜、＝、＞)Ｌ
    ならば、
    　Ｈ(＜、＝、＞)Ｍ
    となっている。
  
  ここで、
  　ＨがＭより大きければ、
  　ＧがＬより大きい。
  なぜなら、
  背理法の仮定として、
  　もし、ＧがＬより大きくないとすれば、
  　公理１ー７の補足（線分・角は大か等か小）
  により、
  　ＧがＬに等しい場合と
  　ＧがＬより小さい場合がなる。
  
  • 　Ｇ＝Ｌ
    または、
    　Ｇ＜Ｌ
    となる。
  
  ＧがＬに等しい場合は、
  　命題の設定により
  　ＨもＭに等しくなるので、
  　不可能である。
  
  • 　Ｈ＝Ｍ
    となり、
    　Ｈ＞Ｍ
    と矛盾する。
  
  ＧがＬより小さい場合、
  　命題の設定により
  　ＨもＭより小さくなるので。
  　不可能である。
  
  • 　Ｈ＜Ｍ
    となり、
    　Ｈ＞Ｍ
    と矛盾する。
  
  したがって
  　背理法により、
  　ＧはＬより大きい。
  
  • 　Ｇ＞Ｌ
    となっている。
  
  等しい場合、小さい場合も
  　同様に証明できる。
  したがって、
  　Ｃ、Ａの［任意の］同数倍Ｈ、Ｇと、
  　Ｄ、Ｂの別の任意の同数倍Ｍ、Ｌが
  　とられていて
  　ＨがＭより大きければ、
  　ＧもＬより大きく、
  　等しければ、等しく、
  　小さければ、小さい。
  
  • 　Ｈ(＜、＝、＞)Ｍ
    ならば、
    　Ｇ(＜、＝、＞)Ｌ
    となっている。
  
  定義５ー５（同じ比）
  により
  　ＣがＤに対するように、
  　ＡがＢに対する。
  
  • 　Ｃ：Ｄ＝Ａ：Ｂ
    となっている。
  
  

　
これが証明すべきことであった。

• 命題５ー１１の補足は、
  　Ａ：Ｂ＝Ｃ：Ｄ
  ならば
  　Ｃ：Ｄ＝Ａ：Ｂ
  のことである。
  　
• 等しい量は等しい量に対し同じ比をもつ。
  以下、命題５ー１１の補足２（等しい量は同じ比をもつ）という。
  命題５ー７ により
  　Ａ＝ＢならＡ：Ｃ＝Ｂ：Ｃ
  　Ｃ＝ＤならＢ：Ｃ＝Ｂ：Ｄ
  命題５ー１１ により
  　Ａ：Ｃ＝Ｂ：Ｄとなる。
  
  
• 命題５ー１１は、
  　Ａ：Ｂ＝Ｃ：Ｄ、Ｃ：Ｄ＝Ｅ：Ｆ
  ならば
  　Ａ：Ｂ＝Ｅ：Ｆ
  のことである。
  　
• 命題５ー１１の補足は推論用命題である。

  前提	作図	推論
  定義		5-5
  公準
  公理		1-7補
  命題
  その他		背理法

  
  
  
• 命題５ー１１の補足２は推論用命題である。

  前提	作図	推論
  定義
  公準
  公理
  命題		5-7,5-11
  その他

  
  　
• 命題５ー１１は推論用命題である。

  前提	作図	推論
  定義		5-5
  公準
  公理
  命題	補(義5-2)	5-11補
  その他		コ2(題5-4)

前 　　 次 　　 目次 　　頁頭