ユークリッド原論をどう読むか（９509）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第５巻

命題５ー９（同一比の量）
同一の量に対して
　同じ比をもつ量は
　互いに等しい。
そして
　同一の量が
　それらに対して同じ比をもつ量は
　互いに等しい。
　

• 量は、定義５ー１の補足 による。
• 同じ比は、定義５ー５ による。
• 等しいは、公理１ー７ による。

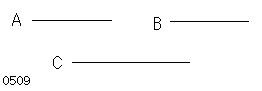
Ａ、Ｂの双方が
　Ｃに対し
　同じ比をもつとせよ。

• 同じ比をもつ線分の作図（仮想的）は
  　コメント２（命題５ー４）参照のこと。
• 　Ａ：Ｃ＝Ｂ：Ｃ
  となっている。

ＡはＢに等しい
　と主張する。
　
もし
　等しくなかったら

• 背理法の仮定である。
• 　Ａ≠Ｂ
  としている。

　Ａ、Ｂの双方は
　Ｃに対し同じ比をもたなかったであろう。

• 命題５ー８（量の大小と比の大小）
  による。
• 　Ａ＞Ｂ
  ならば、
  　Ａ：Ｃ＞Ｂ：Ｃ
  となり、
  　Ａ＜Ｂ
  ならば、
  　Ａ：Ｃ＜Ｂ：Ｃ
  となっている。
  

ところが
　もっている。

• 命題の設定 による。
• 　Ａ：Ｃ＝Ｂ：Ｃ
  となっている。

したがって
　ＡはＢに等しい。

• 背理法による。

また
　ＣがＡ、Ｂの双方に対し
　同じ比をもつとせよ。

• 　Ｃ：Ａ＝Ｃ：Ｂ
  となっている。

ＡはＢに等しい
　と主張する。
　
もし
　等しくなかったら、

• 背理法の仮定である。
• 　Ａ≠Ｂ
  としている。

　Ｃは
　Ａ、Ｂの双方に対し
　同じ比をもたなかったであろう。

• 命題５ー８（量の大小と比の大小）
  による。
• 　Ａ＞Ｂ
  ならば、
  　Ｃ：Ａ＜Ｃ：Ｂ
  となり、
  　Ａ＜Ｂ
  ならば、
  　Ｃ：Ａ＞Ｃ：Ｂ
  となっている。
  

ところが
　もっている。

• 命題の設定による。
• 　Ｃ：Ａ＝Ｃ：Ｂ
  となっている。

したがって
　ＡはＢに等しい。

• 背理法による。

　
よって
　同一の量に対して
　同じ比をもつ量は互いに等しい。
そして
　同一の量が
　　それらに対して同じ比をもつ量は
　互いに等しい。
これが証明すべきことであった。

• 命題５ー７（同一量の比）
  の逆である。
• 命題５ー９は、
  　Ａ：Ｃ＝Ｂ：Ｃ
  ならば、
  　Ａ＝Ｂ、
  　Ｃ：Ａ＝Ｃ：Ｂ
  ならば、
  　Ａ＝Ｂ
  のことである。
• 命題５ー９は推論用命題である。

  前提	作図	推論
  定義
  公準
  公理
  命題		5-8
  その他		背理法,コ2(題5-4)

前 　　 次 　　 目次 　　頁頭