ユークリッド原論をどう読むか（１）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論
第１巻

命題１ー３（作図・等しい線分を切り取る）　
（作図・等しい線分となる点）
　二つの不等な線分が与えられた
とき、
　大きいものから
　小さいものに等しい線分を
　切り取ること。

• そもそも
  　二つの線分が不等である
  　ことが
  　なぜわかるのか
  という、
  　前提に関する疑問が生じる。
  
  　一方の線分を、
  　他方の線分と端点を共有する
  ように、
  　命題１ー２（作図・線分）
  により移動し、
  　共有する端点を中心に、
  　移動してきた線分を半径として
  　公準１ー３（作図.円）
  により
  　円を描く。
  
  　他方の線分が
  　円内に収まっていれ
  ば、
  　定義１ー１５（円）
  により
  　収まっている線分が
  　小さい方である
  と分かる。
  
  　描いた円が
  　他方の線分と交わっていれ
  ば、
  　定義１ー１５（円）
  により
  　交わっている線分が
  　大きい
  と分かる。
• 　不等は、定義の補足（公理１ー４） による。
• 　線分は、定義の補足（命題１ー１） による。
• 　大きいは、公理１ー８ による。
• 　小さいは、公理１ー８の補足 による。
• 　等しいは、公理１ー７ による。

　与えられた二つの不等な線分をＡＢ、ＣＤ
とし、
　そのうちＡＢが大きい
とせよ。

• 　ＡＢ＞ＣＤ
  となっている。

このとき
　大きいものＡＢから
　小さいものＣＤに等しい線分を
　切り取ら
ねばならぬ。
　
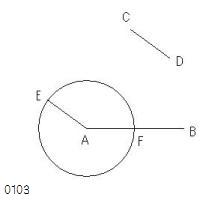
　点Ａにおいて
　線分ＣＤに等しく
　ＡＥがつくられた
とせよ。
　　　　　　【・・・(a)】

• 　命題１ー２（作図・線分） による。
• 　Ｅ；（線分ＡＥ＝線分ＣＤ）
  となっている。

そして
　中心Ａ、半径ＡＥをもって
　円ＥＦＧが描かれた
とせよ。
　　　　　　【・・・(b)】

• 　公準１ー３（作図.円） による。
• 　Ｆ；交点（ＡＢ、円（Ａ、ＡＥ））、
  　Ｇ；（円ＥＦＧ；円（Ａ、ＡＥ））
  となっている。
• 　命題の設定により、
  　ＡＢはＣＤより大きい
  ので、
  　円は線分ＡＢとＡＢ上の点Ｆで交わる。
  　この補足的な証明は次の通りである。
  
  　Ｂは円の外部にある。
  　背理法の仮定として
  もし
  　Ｂが円の内部にあれ
  ば、
  　公準１ー２（作図.直線の延長）
  により、
  　２点Ａ、Ｂを結ぶ線分を
  　Ｂ方向に延長して
  　円と交わる点をＨ
  とすれば、
  　定義１ー１５（円）
  により
  　ＡＨはＡＥに等しく、
  　ＡＥはＣＤに等しい
  から
  　公理１ー１（同じものに等しい）
  により
  　ＡＨはＣＤに等しい。
  　公理１ー８（大きい）
  により
  　ＡＨはＡＢより大きい。
  よって、
  　公理１ー８の補足（小さい）
  により
  　ＣＤはＡＢより大きい。
  　これは
  　ＡＢがＣＤより大きい
  　という命題の条件に矛盾する。
  したがって
  　背理法により、Ｂは円の外部にある。
  　Ａは
  　その円の内部にある
  ので、
  　線分ＡＢは
  　円の内部と外部とを結ぶ線である。
  　定義１ー１５（円）
  により
  　円は境界（端）で囲まれた図形である
  から、
  　線分ＡＢは境界（端）を通る。
  　定義１ー３（線の端）
  により
  　線の端は点である
  から、
  　線分ＡＢは点を通る。
  　この点をＦとする。
  原論では、
  　このＦを最初から図に描き込んで
  　推論している。
  そのため
  　筋道が混乱して見える。

そうすれば
　点Ａは円ＥＦＧの中心である

• 　(b)による。
• 　Ａ＝中心.円ＥＦＧ
  となっている。

から、
　ＡＦはＡＥに等しい。
　　　　　　【・・・(1)】

• 　前節、
  　定義１ー１５（円）
  による。
• 　ＡＦ＝ＡＥ
  となっている。

ところが、
　ＣＤもＡＥに等しい。

• 　(a) による。
• 　ＣＤ＝ＡＥ
  となっている。

それゆえ、
　ＡＦ、ＣＤの双方はＡＥに等しい。

• 　前節、前々節による。
• 　ＡＦ＝ＡＥ、ＣＤ＝ＡＥ
  となっている。

したがって
　ＡＦもＣＤに等しい。

• 　前節、
  　公理１ー１（同じものに等しい） による。

よって
　二つの不等な線分ＡＢ、ＣＤが
　与えられた
とき、
　大きいものＡＢから
　小さいものＣＤに等しいＡＦが
　切り取られた。

　これが作図すべきものであった。

• 　この命題は、
  　大きい線分上に点をとり、
  　端からその点までの線分が
  　小さい線分に等しくなるようにできる。
  という意味でみることができる。
  　（以下、命題１ー３の補足（作図.等しい線分となる点）という。）
• 　この命題は、
  　公理１ー７の補足（線分・角は大か等か小）の証明と
  　内容的に重なっている
  と見ることができる。
  もし、
  　2直線ＡＢ、ＣＤが等しくなけれ
  ば、
  　点Ａにおいて
  　線分ＣＤに等しくＡＥがつくられる。
  そして、
  　中心Ａ、半径ＡＥをもって
  　円ＥＦＧを描くことができる。
  　点Ｂは
  　円ＥＦＧの内部か外部かいずれかにある。
  　内部にあれ
  ば、
  　線分ＣＤがＡＢより大きく、
  　外部にあれ
  ば、
  　線分ＡＢがＣＤより大きい
  と証明される。
  そこで、
  　ＡＢがＣＤより大きい場合に、
  　ＡＢ上に点Ｈをとり、
  　ＡＨとＣＤが等しくなるようにできる
  というのが命題１ー３である。
  例えば、
  　命題１ー５（２等辺三角形の底角） にこの用例がある。
• 　命題1-3は、
  　線分ＡＢ、ＣＤ；ＡＢ＞ＣＤ
  に対して、
  　Ｅ；線分ＡＥ＝ＣＤ、
  　Ｆ；交点(ＡＢ、円(Ａ、ＡＥ))
  をとるならば、
  　ＡＦ＝ＣＤ
  のことである。
  
• 命題１ー３の補足（作図.等しい線分となる点）

  前提	作図	推論
  定義
  公準
  公理
  命題	1-3
  その他

• 　命題1-3は作図用命題である。

  前提	作図	推論
  定義		1-3、1-15
  公準	1-2、1-3
  公理		1-1、1-8、1-8補
  命題	1-2
  その他		公理1-7補 の証明の一部である。

前 　　 次 　　 目次 　　頁頭