ユークリッド原論をどう読むか（１０）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第６巻

命題６ー１３（作図.２線分の比例中項）
(比例中項は２項の間)
与えられた２線分の
　比例中項を見いだすこと。

• 線分は、 定義の補足（命題１ー１） による。
• 比例中項は、 定義の補足３（命題６ー８） による。

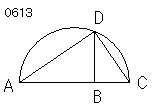
与えられた２線分を
　ＡＢ、ＢＣとせよ。

• 命題６ー１０の補足（区分線分の端点共有化）
  により、
  　端点を共有できる。
• 　線分ＡＢ、ＢＣ
  をとっている。

このとき
　ＡＢ、ＢＣの
　比例中項を見いださねばならぬ。
　
それらが１直線をなすようにおかれ、

• 公準１ー２（作図.直線の延長）
  により、
  　線分ＡＢを
  　Ｂの方向に延長する。
  命題１ー３の補足（作図.等しい線分となる点）
  により、
  　点Ｃ’を、
  　延長した部分に、
  　ＢＣ’がＢＣと等しくなるようにとり、
  　Ｃ’を改めてＣとして、
  　溯って用いている。
• 　Ｃ'(延長ＡＢ;;ＢＣ'＝ＢＣ)、
  をとり、
  　Ｃ'をＣ
  としている。 　

　ＡＣ上に半円ＡＤＣが描かれ、

• 命題１ー１０（作図・線分の２等分）
  により、
  　線分ＡＣの２等分点Ｅを求め、
  公準１ー３（作図.円）
  により、
  　Ｅを中心、ＡＣを直径とする半円を描く。
• 　半円[ＡＣ]
  をとっている。

　点Ｂから
　線分ＡＣに直角にＢＤがひかれ、

• 命題１ー１１（作図・線分からの垂線）
  による。
• 　Ｄ(半円[ＡＣ];;ＢＤ⊥ＡＣ)
  をとっている。

　ＡＤ、ＤＣが結ばれたとせよ。

• 公準１ー１（作図.直線）
  による。
• 　ＡＤ、ＤＣ
  をとっている。

角ＡＤＣは
　半円内の角であるから、
　直角である。

• 命題３ー３１（半円内の角は直角、半円より大小の切片内の角、切片の角）
  による。
• 　∠ＡＤＣ＝∠Ｒ
  となっている。

そして
　直角三角形ＡＤＣにおいて
　直角から底辺に
　垂線ＤＢが下されたから、
　ＤＢは
　底辺の２部分ＡＢ、ＢＣの比例中項である。

• 命題６ー８（直角三角形の垂線と相似）
  による。
• 　ＡＢ：ＢＤ＝ＢＤ：ＢＣ
  となっている。

よって
　与えられた２線分ＡＢ、ＢＣの
　　比例中項ＤＢが見いだされた。
これが作図すべきものであった。

• 命題６ー１３は、
  　ＡＢ、ＢＣ
  に対して、
  　Ｃ'(延長ＡＢ;;ＢＣ'＝ＢＣ)、
  　Ｄ[半円[ＡＣ'];;ＢＤ⊥ＡＣ']
  をとれば、
  　ＡＢ：ＢＤ＝ＢＤ：ＢＣ
  のことである。
  
• 　作図による比例中項の構成過程により、
  　比例中項ＢＤは直径ＡＢ＋ＢＣの半分より小さい。
  　したがって、
  　　ＡＢ、ＢＣの大きい方より小さく、
  　定義５ー５（同じ比）
  により、
  　　小さい方より大きい。
  よって、
  　比例中項は、
  　　それを構成する２項が異なれば、
  　　一方より大きく、一方より小さい
  (以下、命題６ー１３の補足(比例中項は２項の間)という。)
• 命題６ー１３の補足(比例中項は２項の間)

  前提	作図	推論
  定義		5-5,補3(題6-8)
  公準
  公理
  命題	6-13
  その他

  
  
• 命題６ー１３は作図用命題である。

  前提	作図	推論
  定義
  公準	1-1,1-2,1-3
  公理
  命題	1-3補,1-10,1-11,6-10補	3-31,6-8
  その他

前 　　 次 　　 目次 　　頁頭