偺徹柧傪怳傝曉傞偲丄
丂岞弨侾乕俆乮暯峴慄岞弨乯
丂乮柦戣侾乕俀俋乮暯峴偲嶖妏丄撪懳妏丄摨懁撪妏乯丄
丂柦戣侾乕俁侽乮暯峴偺暯峴乯丄
丂柦戣侾乕俁侽偺曗懌(岎慄偵暯峴側慄) 乯
丂傪慜採偲偟偰偄側偄丅
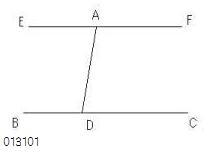
揰俙偲捈慄俛俠偵偮偄偰丄
丂捈慄俛俠忋偺揰俢傪寛傔偨偲偒丄
丂嶖妏偺摍偟偄暯峴慄傪堷偔偙偲偑偱偒傞
丂偲偄偆傕偺偱偁傞丅
偁傞偄偼丄
丂暯峴慄偑堦偮偼偁傞
丂偲偄偆傕偺偱偁傞丅
丂
偦偙偱丄
丂師偺媈栤偑惗偠傞丅
丂
嘆捈慄俛俠忋偺暿偺揰俧傪寛傔偨偲偒丄
丂嶖妏偺摍偟偄暯峴慄傪
丂傂偔偙偲偑偱偒傞偑丄
丂偙偺暯峴慄偼
丂揰俢傪寛傔偨偲偒偺暯峴慄偲摨堦偐丅
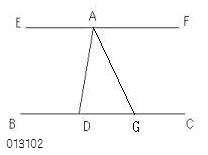
嘇偙傟埲奜偵暯峴慄偼側偄偐丅
岞弨侾乕俆乮暯峴慄岞弨乯
傪慜採偲偡傞偲丄
丂嘆嘇偑峬掕揑偵夝寛偝傟傞丅
嘆偵偮偄偰偼丄
丂柦戣侾乕俁俀乮嶰妏宍偺撪懳妏丒撪妏偺榓乯
傪嶲徠偝傟偨偄丅
嘇偵偮偄偰偼丄
丂師偺夝愢傪嶲徠偝傟偨偄丅
傪慜採偲偡傞偲丄
丂偙偺柦戣侾乕俁侾乮嶌恾丒暯峴慄乯
偵
丂暯峴慄偑桞堦偱偁傞偙偲傪
丂晅偗壛偊傞偙偲偑偱偒傞丅
偡側傢偪丄
丂梌偊傜傟偨揰傪捠傝丄
丂梌偊傜傟偨捈慄偵暯峴慄傪傂偔偙偲偑偱偒傞丅
暯峴慄偼桞堦偙傟偩偗偱偁傞丅
丂乮埲壓丄柦戣侾乕俁侾偺曗懌(梌揰傪捠傞暯峴慄偼桞堦)偲偄偆丅乯
攚棟朄偺壖掕偲偟偰丄
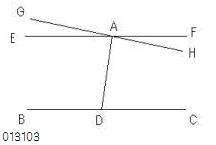
丂傕偟
丂揰俙傪捠傝捈慄俛俠偵暯峴側捈慄偑
丂俤俥埲奜偵俧俫偑偁傞偲偡傞丅
攚棟朄偺壖掕偵傛傝
丂俤俥偲俧俫偼揰俙偱岎傢傞丄
丂堎側傞捈慄偱偁傞丅
柦戣偺壖掕偵傛傝
丂俛俠偲俤俥偼暯峴偱偁傞丅
柦戣侾乕俁侽偺曗懌(岎慄偵暯峴側慄)
偵傛傝
丂俛俠偲俧俫偼岎傢傞丅
偲偙傠偑
丂攚棟朄偺壖掕偵傛傝
丂俛俠偲俧俫偼暯峴偱偁傞偐傜丄
丂柕弬偲側傞丅
攚棟朄偵傛傝
丂俤俥偲俧俫偼堦抳偡傞丅
岞弨侾乕俆乮暯峴慄岞弨乯
傪慜採偲偡傞尨榑偺柦戣偲偟偰偼丄
丂偙偺曗懌偺曽偑
丂柦戣偲偟偰偼朷傑偟偄偲峫偊傜傟傞丅
偐傜
丂岞弨侾乕俆乮暯峴慄岞弨乯
傪摫偔偙偲偑偱偒傞丅
俀捈慄俙俛丄俠俢偵捈慄俤俥偑
丂俀揰俧丄俫偱偦傟偧傟岎傢偭偰偍傝丄
丂妏俛俧俫丄俧俫俢偺摨懁撪妏偺榓偑
丂俀捈妏傛傝彫偝偄傕偺偲偡傞丅
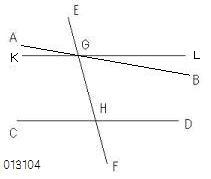
俧傪捠傝
丂俠俢偵暯峴側捈慄俲俴傪丄
丂柦戣侾乕俁侾乮嶌恾丒暯峴慄乯
偵傛傝丄
丂嶖妏俧俫俠偲俴俧俫偑摍偟偔側傞傛偆偵丄
丂偟偨偑偭偰
丂妏俴俧俫偲妏俧俫俢偺榓偑
丂俀捈妏偲側傞傛偆偵丄
丂昤偔丅
崱丄
丂妏俛俧俫偲妏俧俫俢偺榓偼
丂俀捈妏傛傝彫偝偄偺偱丄
丂岞棟侾乕係偺曗懌俀乮晄摍側傕偺偐傜摍偟偄傕偺傪傂偔乯
偵傛傝
丂妏俴俧俫傛傝妏俛俧俫偼彫偝偄丅
偟偨偑偭偰
丂俀捈慄俙俛丄俲俴偼
丂揰俧偱岎傢傞堎側傞捈慄偱偁傝丄
丂敿捈慄俧俛偼
丂捈慄俲俴偵偮偄偰捈慄俠俢偲摨偠懁偵丄
丂敿捈慄俧俙偼
丂斀懳懁偵偁傞丅
俲俴偼丄
丂柦戣侾乕俁侾偺曗懌(梌揰傪捠傞暯峴慄偼桞堦)
偵傛傝丄
丂俧傪捠傞俠俢偺桞堦偺暯峴慄偱偁傞偐傜丄
丂俙俛偼俠俢偲岎傢傝丄
丂偟偐傕丄
丂敿捈慄俧俛偑捈慄俲俴偵偮偄偰
丂捈慄俠俢偲摨偠懁偵偁傞偺偱丄
丂摨懁撪妏偺榓偑
丂俀捈妏傛傝彫偝偄懁偱岎傢傞丅
傛偭偰
丂岞弨侾乕俆乮暯峴慄岞弨乯
偑惉棫偡傞丅
偲柦戣侾乕俁侾偺曗懌(梌揰傪捠傞暯峴慄偼桞堦)
偼摨抣偱偁傞丅
偐傜丄
丂柦戣侾乕俁侽偺曗懌(岎慄偵暯峴側慄)
傪摫偔偙偲偑偱偒傞丅
丂
揰俤傪捠傝俥俧偵暯峴側捈慄偼丄
丂柦戣侾乕俁侾偺曗懌(梌揰傪捠傞暯峴慄偼桞堦)
偵傛傝
丂俙俛偩偗偱偁傞丅
偟偨偑偭偰
丂俠俢偼俥俧偲岎傢傞丅
傛偭偰
丂柦戣侾乕俁侽偺曗懌(岎慄偵暯峴側慄)
偑惉棫偡傞丅
偐傜
丂柦戣侾乕俁侾偺曗懌(梌揰傪捠傞暯峴慄偼桞堦)
傪摫偔偙偲偑偱偒傞丅
丂
攚棟朄偺壖掕偲偟偰丄
丂揰俙傪捠傝捈慄俛俠偵暯峴側丄
丂堎側傞俀捈慄俤俥丄俧俫偑偁偭偨偲偡傞丅
俤俥丄俧俫偼
丂俙偱岎傢傝丄
丂俤俥偼俛俠偵暯峴偱偁傞偐傜丄
丂柦戣侾乕俁侽偺曗懌(岎慄偵暯峴側慄)
偵傛傝
丂俧俫偼俛俠偲岎傢傞丅 偙傟偼丄
丂攚棟朄偺壖掕偵柕弬偡傞丅
傛偭偰
丂柦戣侾乕俁侾偺曗懌(梌揰傪捠傞暯峴慄偼桞堦)
偑惉棫偡傞丅
偲柦戣侾乕俁侾偺曗懌(梌揰傪捠傞暯峴慄偼桞堦)
偼摨抣偱偁傞丅
丂偦傟偧傟偺悅慄偼岎傢傞丅
丂乮埲壓丄偙傟傪柦戣侾乕俁侾偺曗懌俀(岎慄偺悅慄)偲偄偆丅乯
埲壓偺傛偆偵徹柧偝傟傞丅
丂
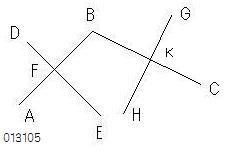
慄暘俙俛偲俛俠偑
丂岎傢偭偰偄傞丅
偙偺偲偒丄
丂攚棟朄偺壖掕偲偟偰丄
丂傕偟俢俤偲俧俫偑岎傢傜側偄偲偡傟偽丄
丂慄暘俙俛偺悅慄俢俤偲
丂慄暘俛俠偺悅慄俧俫偼
丂暯峴偲側傞丅
柦戣侾乕俁侽偺曗懌(岎慄偵暯峴側慄)
偵傛傝
丂俙俛偼俧俫偲岎傢傝丄
丂柦戣侾乕俀俋乮暯峴偲嶖妏丄撪懳妏丄摨懁撪妏乯
偵傛傝
丂俙俛偼俧俫偲悅捈偲側傞丅
柦戣侾乕俀俉乮撪懳妏丄摨懁撪妏偲暯峴乯
偵傛傝
丂俙俛偲俛俠偼暯峴偲側傞丅
掕媊侾乕俀俁乮暯峴(慄)乯
偵傛傝
丂俙俛偲俛俠偼岎傢傜側偄丅
偙傟偼
丂柦戣偺壖掕偵柕弬偡傞偐傜丄
丂攚棟朄偵傛傝
丂岎傢傞俀慄暘偺偦傟偧傟偺悅慄偼
丂岎傢傞丅
柦戣侾乕俁侾偺曗懌(梌揰傪捠傞暯峴慄偼桞堦)丄
岞弨侾乕俆乮暯峴慄岞弨乯
偼摨抣偱偁傞丅
丂捈慄俛俠丄
丂揰俙[俛俠奜]
偵懳偟偰丄
丂捈慄俤俥(俙,俤俥乤俛俠);桞堦
偺偙偲偱偁傞丅
丂捈慄俛俠丄
丂揰俙[俛俠奜]
偵懳偟偰丄
丂揰俢[俛俠]丄
丂揰俤[佢俢俙俤亖佢俙俢俠,俙俢偵偮偄偰俠偲斀懳懁]丄
丂揰俥[墑挿俤俙]丄
丂捈慄(俤,俥)
傪偲傟偽丄
丂俤俥乤俛俠
偺偙偲偱偁傞丅
| 慜採 | 嶌恾 | 悇榑 |
| 掕媊 | 1-23 | |
| 岞弨 | ||
| 岞棟 | ||
| 柦戣 | 1-28 , 1-29 , 1-30曗 | |
| 偦偺懠 | 攚棟朄 |
| 慜採 | 嶌恾 | 悇榑 |
| 掕媊 | ||
| 岞弨 | ||
| 岞棟 | ||
| 柦戣 | 1-30曗 | |
| 偦偺懠 | 攚棟朄 |
| 慜採 | 嶌恾 | 悇榑 |
| 掕媊 | ||
| 岞弨 | 1-1丄1-1曗丄1-2 | |
| 岞棟 | ||
| 柦戣 | 1-23 | 1-27 |
| 偦偺懠 |