ユークリッド原論をどう読むか（３）
頁末 　　 前 　　 次 　　 目次　

ユークリッド原論
第１巻

命題１ー３０（平行の平行）　
(交線に平行な線)
同一の直線に平行な２直線は
　また互いに平行である。

• 直線は、定義１ー４による。
• 平行は、定義１ー２３による。

直線ＡＢ、ＣＤの双方が
　ＥＦに平行であるとせよ。

• 　ＡＢ‖ＥＦ、
  　ＣＤ‖ＥＦ
  としている。

ＡＢはＣＤに平行であると主張する。

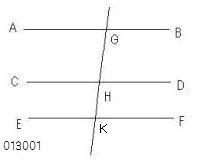
直線ＧＫがそれらに交わるとせよ。

• 平行な２直線と交わる直線は
  　存在する。
  なぜなら、
  　公準１ー１の補足（作図.任意の点をとる）
  により
  　それぞれの直線上に１点ずつとり、
  　公準１ー１（作図.直線）
  により２点を結び、
  　公準１ー２（作図.直線の延長）
  により直線に延長すればよい。
  しかし
  　３本目の直線に交わるかどうかは
  　保証がない。
  ここは、
  　原論のギャップである。
  このギャップを埋めるために
  　「異なる２直線が１点で交わるとき、
  　一方の直線に平行な直線は
  　他方の直線と交わり、
  　交点をとることができる。」
  　（以下、命題１ー３０の補足(交線に平行な線)という）
  　を証明する。
  
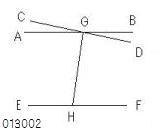
  ２直線ＡＢ、ＣＤがＧで交わり、
  　２直線ＡＢ、ＥＦが平行であるならば、
  　ＣＤとＥＦは交わると主張する。
  ＥＦ上に
  　公準１ー１の補足（作図.任意の点をとる）
  により点Ｈをとり、
  　公準１ー１（作図.直線）
  によりＧとＨを結び
  　ＣＤとＧＨがＧで交わるようにする。
  直線ＣＤは、
  　ＧでＡＢとＧＨと双方に交わるから、
  　定義１ー８の補足（交わる(直線)）
  により
  角ＡＧＨを通る場合]
  角ＢＧＨを通る場合]
  がある。
  
  [ 角ＡＧＨを通る場合]
  ＡＢ、ＥＦは平行だから、
  　命題１ー２９（平行と錯角、内対角、同側内角）
  により
  　角ＢＧＨと角ＧＨＦの和は２直角である。
  今、
  　公理１ー８（大きい）
  により、
  　角ＢＧＨは角ＤＧＨより大きい。
  したがって、
  　公理１ー４（不等なものに等しいものを加える）
  により
  　角ＢＧＨと角ＧＨＦの和は
  　角ＤＧＨと角ＧＨＦの和より大きいので、
  　公理１ー８の補足２（等より大・小、大・小に等）
  により
  　角ＤＧＨと角ＧＨＦの和は２直角より小さい。
  公準１ー５（平行線公準）
  により、
  　２直線ＣＤとＥＧは交わる。
  [ 角ＡＧＨを通る場合]
  角ＡＧＨを通る場合も同様に論証できる。
  ゆえに
  [２つの場合より]
  　２直線ＡＢ、ＣＤがＧで交わり、
  　２直線ＡＢ、ＥＦが平行であるならば、
  　ＣＤとＥＦは交わる。
  これで命題１ー３０の補足が証明された。
• 　公準１ー１の補足（作図.任意の点をとる）
  により、
  　ＣＤ上にＨ、ＥＦ上にＫをとり、
  　公準１ー１（作図.直線）
  によりＨＫを結び、
  　公準１ー２（作図.直線の延長）
  によりＨＫを延長する。
  　命題１ー３０の補足(交線に平行な線)
  により、
  　ＥＦと１点で交わるＨＫは
  　ＥＦに平行なＡＢと交わる。
  その交点をＧとすれば、
  　直線ＥＦと、
  　それに平行な２直線ＡＢ、ＣＤとの３直線に交わる
  　直線ＧＫが存在する。
• 　直線ＧＫ╂(ＡＢ、ＣＤ、ＥＦ)、
  　交点Ｇ(ＧＫ,ＡＢ)、
  　交点Ｈ(ＧＫ,ＣＤ)、
  　交点Ｋ(ＧＫ,ＥＦ)
  をとっている。

　直線ＧＫが
　平行な２直線ＡＢ、ＥＦに交わる
から、
　角ＡＧＫは角ＧＫＦに等しい。
　　　　　　【・・・(1)】

• 　命題１ー２９（平行と錯角、内対角、同側内角）
  による。

また
　直線ＧＫが
　平行な２直線ＥＦ、ＣＤに交わる
から、
　角ＧＨＤは角ＧＫＦに等しい。

• 　命題１ー２９（平行と錯角、内対角、同側内角）
  による。
• 　∠ＧＨＤ＝∠ＧＫＦ
  となっている。

そして
　角ＡＧＫが
　角ＧＫＦに等しいことも証明された。

• (1) による。
• 　∠ＡＧＫ＝∠ＧＫＦ
  となっている。

ゆえに
　角ＡＧＫも角ＧＨＤに等しい。

• 公理１ー１（同じものに等しい）
  による。
• 　∠ＡＧＫ＝∠ＧＨＤ
  となっている。

そして錯角である。

• 定義の補足（命題１ー２７）(錯角)
  による。

したがって
　ＡＢはＣＤに平行である。

• 命題１ー２７（錯角と平行）
  による。
• 　ＡＢ‖ＣＤ
  となっている。

これが証明すべきことであった。

• この命題１ー３０は
  　この命題１ー３０の補足(交線に平行な線)
  により、
  　より簡潔に次のように証明される。
  背理法の仮定として、
  　ＡＢ、ＣＤが平行でないとすると、
  　定義１ー２３（平行(線)）
  により、
  　点Ｌで交わる。
  　ＡＢ、ＥＦが、
  　命題の仮定により平行である
  から、
  　この命題の補足により、
  　ＣＤはＥＦに交わる。
  しかし、
  　ＣＤとＥＦは
  　命題の仮定により平行である
  から、
  　矛盾である。
  背理法により
  　ＡＢ、ＣＤは平行である。
• この命題１ー３０から
  　この命題１ー３０の補足を
  　次のように論証することもできる。
  背理法の仮定として、
  　ＣＤとＥＦが交わらないとすると、
  　ＣＤとＥＦは平行である。
  ＡＢとＥＦは、
  　命題１ー３０の補足の仮定により、
  　平行である。
  したがって
  　ＡＢとＣＤは
  　この命題１ー３０により平行となる。
  しかし、
  　ＡＢとＣＤは
  　この命題の補足の仮定により
  　交わっているから、
  　矛盾である。
  背理法により
  　ＣＤとＥＦは交わる。
• したがって、
  　この命題１ー３０と
  　この命題１ー３０の補足は同値である。
• 命題1-30補は、
  　直線ＡＢ、ＣＤ、ＥＦ
  について、
  　ＡＢ╂ＣＤ、
  　ＡＢ‖ＥＦ
  ならば、
  　ＣＤ╂ＣＤ
  のことである。
  
• 命題1-30は、
  　直線ＡＢ、ＣＤ、ＥＦ
  について、
  　ＡＢ‖ＥＦ、
  　ＣＤ‖ＥＦ
  ならば、
  　ＡＢ‖ＣＤ
  のことである。
  
• 命題１ー３０の補足(交線に平行な線)

  前提	作図	推論
  定義		1-8補
  公準	1-1、1-1補、1-5
  公理		1-4、1-8、1-8補2
  命題		1-29
  その他		背理法、場合分け

• 命題1-30は推論用命題である。

  前提	作図	推論
  定義		補（題1-27）
  公準	1-1、1-1補、1-2
  公理		1-1
  命題		1-27、1-29,1-30補
  その他

前 　　 次 　　 目次 　　頁頭