1.14ユークリッド原論1-14

ユークリッド原論をどう読むか（２）
頁末　　前　　次　　目次　

ユークリッド原論
第１巻

命題１ー１４（直線と２直角２）　
「～以外の」
もし
　任意の直線に対して
　その上の点において
　同じ側にない２直線が
　接角の和を２直角に等しくする
ならば、
　この２直線は
　互いに一直線をなす
であろう。

　直線は定義１ー４による。
　点は定義１ー１による。
　同じ側は、定義１ー７の補足による。
　接角は定義１ー１０の補足による。
　直線は定義１ー４による。
　等しいは公理１ー７による。

　直線ＡＢに対して
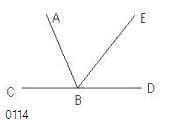
　その上の点Ｂにおいて
　同じ側にない２直線ＢＣ、ＢＤが
　接角ＡＢＣ、ＡＢＤの和を
　２直角に等しくする
とせよ。

　直線ＡＢ、
　点Ｃ[ＡＢ外]、
　直線(Ｃ,Ｂ]、
　Ｄ;(∠ＡＢＣ＋∠ＡＢＤ＝２×∠Ｒ)
をとっている。

　ＢＤはＣＢと一直線をなす
と主張する。

もし
　ＢＤが
　ＢＣと一直線をなすのでない
ならば、

背理法の仮定である。

　ＢＥをＣＢと一直線をなす
とせよ。
　　　　　　【・・・(a)】

　点Ｅ[延長ＣＢ]、
　半直線ＢＥ
をとっている。
　定義１ー７の補足（同じ側・反対側(平面)）
により、
　ＥがＢＤについて
　Ａと同じ側にある場合
　Ａと異なる側にある場合
　がある。

［ＥがＢＤについて
　Ａと同じ側にある場合］

　公準１ー2（作図.直線の延長）
により、
　ＣＢを
　Ｂの方向へ延長した部分を
　ＢＥとする。
　ＥがＢＤについて、
　Ａと同じ側の場合と、
　反対側の場合と
　がある。
以下、
　Ａと同じ側にある場合を論じている。

そうすれば
　直線ＡＢは直線ＣＢＥの上に立つ
から、
　角ＡＢＣ、ＡＢＥの和は２直角に等しい。
　　　　　　【・・・(1)】

　(a),
　命題１ー13（直線と２直角１）
による。
　∠ＡＢＣ＋∠ＡＢＥ＝２×∠Ｒ
となっている。

ところが
　角ＡＢＣ、ＡＢＤの和も２直角に等しい。

　命題の設定 による。
　∠ＡＢＣ＋∠ＡＢＤ＝２×∠Ｒ
となっている。

それゆえ
　角ＣＢＡ、ＡＢＥの和は
　角ＣＢＡ、ＡＢＤの和に等しい。

　(1)、
　公理１ー1（同じものに等しい）
による。
　∠ＡＢＣ＋∠ＡＢＥ
　＝∠ＡＢＣ＋∠ＡＢＤ
となっている。

　双方から
　角ＣＢＡが引き去られた
とせよ。
そうすれば
　残りの角ＡＢＥは
　残りの角ＡＢＤに等しい、

　公理１ー3（等しいものから等しいものをひく）
による。
　∠ＡＢＥ＝∠ＡＢＤ
となっている。

すなわち
　小さいものが大きいものに等しい。

　(a) により、
　直線ＢＥとＢＤが一致していない
から、
　角ＡＢＥと角ＡＢＤのいずれか一方の部分に
　他方がなる。
つまり
　等しくない。

　これは不可能である。
それゆえ
　ＢＥはＣＢと一直線をなさない。

　背理法による。
　Ｅ;延長ＢＥ外
となっている。

　[ＥがＢＤについて
　Ａと異なる側にある場合]
　同様にして
　ＢＤ以外の他のいかなる直線も
　そうならない
ことを証明しうる。
ゆえに
　ＣＢはＢＤと一直線をなす。

　背理法が
　この命題以前にも用いられてきた
が、
　「同様にして
　～以外の他のいかなる～も
　～でないことを証明しうる。」
　という表現は
　初めてである。
　この表現は、
　ＥがＢＤについて
　Ａと反対側にある場合も
　同様に証明できる
　という意味である。
　背理法により、
　点をとる
とき、
　とる位置が
　場合分けされる
ときに
　この表現が
　用いられる。
　以下、コメント（命題１ー１４）(～以外の)という。

よって
　[２つの場合により]
もし
　任意の直線に対して
　その上の点において
　同じ側にない2直線が
　接角の和を2直角に等しくする
ならば、
　この2直線は互いに一直線をなす
であろう。

　これが証明すべきことであった。

命題1-14は、
　直線ＡＢ
について、
　点Ｃ[ＡＢ外]、
　直線(Ｃ,Ｂ]、
　Ｄ;(∠ＡＢＣ＋∠ＡＢＤ＝２×∠Ｒ)
をとるならば、
　Ｄ;延長ＣＢ
ということである。
命題1-14は推論用命題である。

前提作図推論
定義 1-7補
公準 1-2
公理 1-1、1-3
命題 1-13
その他背理法,場合分け,他の～

前　　次　　目次　　頁頭

前提	作図	推論
定義		1-7補
公準	1-2
公理		1-1、1-3
命題		1-13
その他		背理法,場合分け,他の～