ユークリッド原論をどう読むか(3)
頁末
前
次
目次
ユークリッド原論
第1巻
命題1ー34(平行四辺形の対辺・対角・対角線)
平行四辺形・対角線
(平行四辺形と長斜方形とは同義)
(平行四辺形の対角線は互いに他を2等分)
(作図.隣り合う2辺から平行四辺形)
平行四辺形において
対辺および対角は互いに等しく、
対角線はこれを2等分する。
- 平行四辺形とは
向かい合う2組の辺が
それぞれ平行である四辺形をいう。
対角線とは向かい合う角を結ぶ線分をいう。
(以下、定義の補足(命題1ー34)(平行四辺形・対角線)という)
平行四辺形、対角線の用語は初めてここに登場する。
- 対辺、対角は、定義1ー22の補足による。
- 等しいは、公理1ー7による。
- 等分は、定義の補足(公理1ー6)による。
ACBDを平行四辺形とし、
BCをその対角線とせよ。
平行四辺形ACBDの対辺および対角は
互いに等しく、
対角線BCは平行四辺形ACDBを
2等分すると主張する。
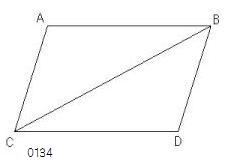
ABはCDに平行であり、
線分BCがそれらに交わっているから、
錯角ABC、BCDは互いに等しい。
【・・・(1)】
- 命題1ー29(平行と錯角、内対角、同側内角)
による。
-
∠ABC=∠BCD
となっている。
またACはBDに平行であり、
BCがそれらに交わっているから、
錯角ACB、CBDは互いに等しい。
- 命題1ー29(平行と錯角、内対角、同側内角)
による。
-
∠ACB=∠CBD
となっている。
このときABC、BCDは
2角ABC、BCAが
2角BCD、CBDにそれぞれ等しく、
1辺が1辺に等しい。
- (1)
にもよる。
-
(∠ABC,∠BCA)=(∠BCD,CBD)、
BC=BC
となっている。
すなわち
等しい角にはさまれる辺BCを共有する
二つの三角形である。
それゆえ
残りの2辺も
残りの2辺にそれぞれ等しく、
残りの角も残りの角に
等しいであろう。
- 命題1ー26(2角挟辺相等)
である。
-
△ABC≡△BCD
となっている。
ゆえに
辺ABはCDに、
ACはBDに等しく、
また
角BACは角CDBに等しい。
【・・・(2)】
-
前節による。
-
AB=CD、
AC=BD、
∠BAC=∠CDB
となっている。
そして
角ABCは角BCDに等しく、
角CBDは角ACBに等しいから、
角ABD全体は角ACD全体に等しい。
- 公理1ー2(等しいものに等しいものを加える)
による。
-
∠ABD=∠ACD
となっている。
しかも
角BACが
角CDBに等しいことも先に証明された。
- (2)
による。
-
∠BAC=∠CDB
となっている。
よって
平行四辺形の対辺および対角は互いに等しい。
《ついで
対角線が
平行四辺形を2等分すると主張する。
ABはCDに等しく、
BCは共通なのであるから
2辺AB、BCは2辺CD、BCに
それぞれ等しい。
そして
角ABCは角BCDに等しい。》
- 命題1ー4(2辺挟角相等)
による。
しかし、すでに
命題の前半を
いわゆる2角挟辺相等の命題1ー26(2角挟辺相等)
により
証明している。
命題1ー26の補足(2角挟辺相等による合同)
から明らかなように、
この部分は本来必要がない。
ここであえて
命題1ー4(2辺挟角相等)
を持ち出す意味を考えると、
証明過程で
命題1ー4(2辺挟角相等)
は重ね合わせをしているが、
命題1ー26(2角挟辺相等)
は重ね合わせをしていない
ためであろう。
いわゆる2辺挟角相等の命題1ー4(2辺挟角相等)
に対する
ユークリッドのこだわりが感じられる。
すなわち、
命題1ー4(2辺挟角相等)
には
2つの三角形が等しい
という文言を入れているが、
本来入れていても何の不思議もない
命題1ー8(3辺相等2)、
命題1ー26(2角挟辺相等)
には
入れていないということである。
《それゆえ
底辺ACもDBに等しい。
そして》
[また、]三角形ABCは三角形BCDに等しい。
よって
対角線BCは平行四辺形ABCDを2等分する。
- 2等分という意味が、
二つの合同な図形に分割できるという意味と、
二つの面積が等しい図形に分割できるという意味と
2通りに考えられる。
次の命題1ー35(平行四辺形の等積変形1)
で
面積が等しいという意味であることが明確になる。
面積については
定義の中で触れられていない。
原論としては、
公理1ー7等しい)
で互いに重なり合うものは
等しいというものの中に、
図形を切り貼りして重なり合うという意味も
含めているようである。
これが証明すべきことであった。
- この命題によって
平行四辺形が
原論の定義1ー22(正方形・矩形・菱形・長斜方形・トラペジオン)
にいう
長斜方形になることが証明された。
逆に長斜方形は、
対角線を一つひいてできる、
二つの三角形が
定義1ー22(正方形・矩形・菱形・長斜方形・トラペジオン)
により
2辺とその間の角が等しいことから、
命題1ー4(2辺挟角相等)
により
合同となる。
その結果、
2組の錯角が等しいことから、
命題1ー27(錯角と平行)
により
向かい合う辺が2組とも平行となり、
平行四辺形であることがわかる。
よって、
平行四辺形と長斜方形とは同義である。
(以下、命題1ー34の補足2(平行四辺形と長斜方形とは同義)という。)
- 定義1ー19の補足3(凸多角形)
により、
平行四辺形の任意の角について、
その対角及び対角線は
2つの辺の間にある。
したがって、
対角線BCについて、
点A、Dは
異なる側にあるので
公準1ー1(作図.直線)
により対角線ADをひくと
命題の補足2(定義1ー14)(図形と直線の交点)
により
2つの対角線BCとADとは交わる。
その交点をEとすると、
三角形ABEとDCEについて、
本命題により
ABとDCが等しく、
また
命題1ー29(平行と錯角、内対角、同側内角)
により
角EAB、EBAとEDC、ECDとが
それぞれ等しいので、
命題1ー26の補足(2角挟辺相等による合同)
により、
2つの三角形は合同であり、
EA、EBとED、ECとが
それぞれ等しい。
したがって、
平行四辺形において、
2つの対角線は
互いに他を2等分する。
(以下、命題1ー34の補足3(平行四辺形の対角線は互いに他を2等分)という。)
-
2線分AB、ACがAで交わっている
ならば
これらを隣り合う2辺とする
平行四辺形ABDC
を作図することができる。
(以下、命題1ー34の補足4
(作図.隣り合う2辺から平行四辺形)という。)
命題1ー31(作図・平行線)
により、
Bを通りACに平行に
直線をひき、
また、
Cを通りABに平行に
直線をひく
と、
命題1ー30の補足(交線に平行な線)
により、
2直線は交わる。
その交点をD
とすると、
定義の補足(命題1ー34)(平行四辺形)
により、
四角形ABDCは平行四辺形になっている。
- 命題1-34は、
平行四辺形ACBD
に対して
AB=CD、
AB‖CD、
AC=BD、
AC‖BD
のことである。
今回は、
ここで紙面が尽きてしまった。
前号にも記したところであるが、
原論の命題は
「これが作図すべきものであった。」か
「これが証明すべきことであった。」で証明が終わる。
このことからわかるとおり、
命題は、
作図用のものと推論用のものとに分類できる。
この観点に立てば、
公準や公理も
作図用と推論用に分かれるのではないかと考えて、
各命題のコメントの最後に表としてまとめてある。
ここまで書き進めてきた上で判断するに、
この論考の最初に指摘したこと、
すなわち、
公準は作図に関係し、
公理は推論に関係していることは
間違っていない。
この論考の目的の一つは、
このことの実証である。
もちろん、
公準1ー5(平行線公準)
を
「交点をとることができる」と
また、
公準1ー4(直角は等しい)
も
「任意の点で直角を描くことができる」と
解釈することが前提である。
後一回で
第一巻を終えることができそうに思われる。
お付き合いいただきたい。
- 命題1-34は、
平行四辺形ACBD
に対して
AB=CD、
AB‖CD、
AC=BD、
AC‖BD
のことである。
-
命題1ー34の補足2(平行四辺形と長斜方形とは同義)
-
命題1ー34の補足3(平行四辺形の対角線は互いに他を2等分)
-
命題1ー34の補足4 (作図.隣り合う2辺から平行四辺形)
- 命題1-34は推論用命題である。
前
次
目次
頁頭
