ユークリッド原論をどう読むか(9507)
頁末
前
次
目次
ユークリッド原論
第5巻
命題5ー7(同一量の比)
(系:比例するなら逆も比例)
2つの等しい量は
同一の量に対し、
また
同一の量は
2つの等しい量に対し
同じ比をもつ。
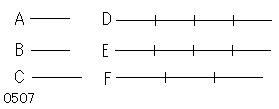
A、Bを等しい2量とし、
Cを別の任意の量とせよ。
A、Bの双方は
Cに対し、
Cは
A、Bの双方に対し、
同じ比をもつと主張する。
A、Bの[任意の]同数倍D、Eと、
Cの別の任意の倍量Fが
とられたとせよ。【・・・(a)】
そうすれば、
DはAの、
EはBの
同数倍であり、
AはBに等しいから、
DもEに等しい。
【・・・(1)】
ところが
Fは別の任意の量である。
それゆえもし
DがFより大きければ、
EもFより大きく、
等しければ、等しく、
小さければ、小さい。【・・・(2)】
- (1),公理1ー1(同じものに等しい)
、
公理1ー8の補足2(等より大・小、大・小に等) という)
による。
-
D(<、=、>)F
ならば、
E(<、=、>)F
となっている。
そして
D、EはA、Bの[任意の]同数倍であり、
FはCの別の任意の倍量である。
したがって
AがCに対するように、
BがCに対する。
次に
Cは
A、Bの双方に対し
同じ比をもつと主張する。
同じ作図がなされたとき、
- 第5巻ではじめて作図の用語が出てきた。
-
量A、C
に対して、
量B(;;B=A)、
D=mA、
E=mB、
F=nC
をとっている。
同様にして
DがEに等しいことを証明しうる。
- (1)である。
-
A=B
により、
D=E=mA=mB
となっている。
ところが
Fは別の量である。
それゆえもし
FがDより大きければ
FはEより大きく、
等しければ、等しく、
小さければ、小さい。【・・・(3)】
- (1),公理1ー1(同じものに等しい)
、
公理1ー8の補足2(等より大・小、大・小に等) という)
による。
-
F(<、=、>)D
ならば、
F(<、=、>)E
となっている。
そして
FはCの[任意の]倍量であり、
D、Eは
A、Bの別の任意の同数倍である。
- (a)による。
-
F=nC、
D=mA、
E=mB
となっている。
ゆえに
CがAに対するように、
CがBに対する。
よって
2つの等しい量は同一の量に対し、
また
同一の量は2つの等しい量に対し
同じ比をもつ。
系
これから次のことが明らかである、
すなわちもし
任意の量が比例するならば、
逆にも比例するであろう。
(以下、命題5ー7の系(比例すれば逆も比例)という。)
- 命題そのものの系というよりは、
A:C=B:Cの論証を、
C:A=C:Bの論証に
切り替える方法にしたがえば、
論証は明らかであるということである。
これが証明すべきことであった。
- 命題5ー7は、
A=B
ならば、
任意のC
に対して、
A:C=B:C、
C:A=C:B
のことである。
-
命題5ー7の系(比例すれば逆も比例)
論証過程は、
命題5−7と同じである。
- 命題5ー7は推論用命題である。
前
次
目次
頁頭
