ユークリッド原論をどう読むか（１）
頁末 　　 前 　　 次 　　 目次　

ユークリッド原論
第１巻

命題１ー８（３辺相等２）　
（３辺相等による合同）
もし
　二つの三角形において
　２辺が２辺にそれぞれ等しく、
　底辺も底辺に等しけれ
ば、
　等しい辺にはさまれた
　角もまた等しい
であろう。

• 　三角形は定義１ー１９の補足２による。
• 　辺は定義１ー１９の補足による。
• 　等しいは公理１ー７による。
• 　底辺は定義１ー２０の補足２による。
• 　角は定義１ー８による。

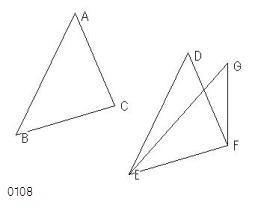
　ＡＢＣ、ＤＥＦを
　２辺ＡＢ、ＡＣが２辺ＤＥ、ＤＦに、
　すなわち
　ＡＢがＤＥに、
　ＡＣがＤＦに
　それぞれ等しい二つの三角形
とせよ。
そして
　底辺ＢＣも底辺ＥＦに等しい
とせよ。

• 　三角(Ａ,Ｂ,Ｃ)、
  　点(Ｅ)、
  　点(Ｆ,ＥＦ＝ＢＣ)
  をとると、
  　命題１ー７の補足(作図.底辺に対する他の２辺の交点)
  により、
  　ＥからＦを見て、
  　ＢからＣを見てＡがある側と同じ側に限定して、
  　点(Ｄ,ＤＥ＝ＡＢ,ＤＦ＝ＡＣ)
  をとっている。
  
• ＡＢ＝ＤＥ、ＡＣ＝ＤＦ、ＢＣ＝ＥＦ
  となっている。

　角ＢＡＣも角ＥＤＦに等しい
と主張する。


　三角形ＡＢＣが
　三角形ＤＥＦに重ねられ、
　点Ｂが点Ｅの上に、
　線分ＢＣがＥＦの上におかれる
ならば、
　ＢＣはＥＦに等しい
から、
　点ＣもＦに重なる
であろう。

• 　定義１ー４（直線）
  により、
  　公理１ー７の補足（線分・角は大か等か小）
  が成立することによる。
• 　重ね合わせの論証方法である。
• 　Ｂ≡Ｅ、Ｃ≡Ｆ、
  　ＢＣ≡ＣＦ
  となっている。

すると［そうすれば］、
　ＢＣがＥＦに重なる
から
　ＢＡ、ＡＣも
　ＥＤ、ＤＦに重なる
であろう。
なぜなら［もし］

• 「なぜならもし」については、
  　コメント（命題１ー４）を参照のこと。

　底辺ＢＣが底辺ＥＦに重なり、
　辺ＢＡ、ＡＣがＥＤ、ＤＦに重ならず、
　ＥＧ、ＧＦのようにずれる
ならば、

• 背理法の仮定である。

　同一の線分上に
　１点において交わる２線分が与えられ、
　それとそれぞれ等しく
　同じ側に異なった点で交わり
　同じ端をもつ
　他の２線分が作られる
ことになるであろう。
ところが
　それはつくられない。

• 命題１ー７（３辺相等１）
  による。

それゆえ
　底辺ＢＣが底辺ＥＦに重ねられる
と、
　辺ＢＡ、ＡＣがＥＤ、
　ＤＦに重ならない
ことはありえない。
ゆえに
　重なるであろう。

• 　背理法による。
• 　(ＢＡ,ＡＣ)≡(ＥＤ,ＤＦ)
  となっている。

したがって
　角ＢＡＣも角ＥＤＦに重なり
　それに等しい
であろう。

• 　前節、
  　公理１ー７（等しい）
  による。
• 　∠ＢＡＣ＝∠ＥＤＦ
  となっている。

よって
もし
　二つの三角形において
　２辺が２辺にそれぞれ等しく、
　底辺も底辺に等しけれ
ば、
　等しい辺にはさまれた角も
　また等しい
であろう。

• 　ここでは、
  　底辺に対する角が等しい
  ことをいっている。

　これが証明すべきことであった。

• 　いわゆる三辺相等の合同条件である。
  しかし、
  　この命題では、
  　２つの三角形が等しい
  ことについては明言していない。
  　対応する２辺とその間の角について、
  　それぞれ等しいことが論証された
  から、
  　命題１ー４（２辺挟角相等）
  により、
  　２つの三角形が等しい
  　ことも証明される。
  すなわち、
  　２つの三角形において
  　３つの辺がそれぞれ等しけれ
  ば、
  　対応する角も等しく、
  　２つの三角形が等しい。
  （以下、命題１ー８の補足（３辺相等による合同）という。）
• 命題1-8の補足は、
  　△ＡＢＣ、ＤＥＦ
  に対して、
  　ＡＢ＝ＤＥ、ＡＣ＝ＤＦ、
  　ＢＣ＝ＥＦ
  ならば、
  　△ＡＢＣ≡△ＤＥＦ
  のことである。
  
• 　この命題についても
  　動かして重ね合わせる証明法であり、
  　特段の作図は行っていない。
  　命題１ー４（２辺挟角相等）
  と同様
  　重ね書き
  と見ることもできる。
• 命題1-8は、
  　△ＡＢＣ、ＤＥＦ
  に対して、
  　ＡＢ＝ＤＥ、ＡＣ＝ＤＦ、
  　ＢＣ＝ＥＦ
  ならば、
  　∠ＢＡＣ＝∠ＥＤＦ
  のことである。
  
• 命題1-8の補足（３辺相等による合同）は推論用命題である。

  前提	作図	推論
  定義
  公準
  公理
  命題		1-4、1-8
  その他		重ね合わせ、背理法

• 命題1-8は推論用命題である。

  前提	作図	推論
  定義		1-4
  公準
  公理		1-7補
  命題	1-7補	1-7
  その他		重ね合わせ、背理法、コ(題1-4)fi

  
  　
  

今回は、
　ここで紙面が尽きてしまった。
第一巻の最後は
　命題48ピタゴラスの定理の逆である。
せめてここまでは書き続けたいと思っている。

前 　　 次 　　 目次 　　頁頭