0607ユークリッド原論６

ユークリッド原論をどう読むか（１０）
頁末　　前　　次　　目次

ユークリッド原論

第６巻

命題６ー７（２辺が比例、挟角以外が等しくて等角となる場合）
（作図.２辺が比例、挟角以外が等しい三角形）
もし
　２つの三角形が
　１つの角が互いに等しく、
　もう一つの角をはさむ辺が比例し、
　残りの角の双方が共に直角より小さいか、
　または
　共に小さくないならば、
　２つの三角形は等角であり、
　比例する２辺にはさまれる角は等しいであろう。

三角形は、定義１ー１９の補足２ による。
角は、定義１ー８ による。
等しくは、公理１ー７ による。
辺は、定義１ー１９の補足 による。
比例は、定義５ー６ による。
直角は、定義１ー１０ による。
小さいは、公理１ー８の補足 による。
等角は、定義の補足（命題４ー２） による。

ＡＢＣ、ＤＥＦを
　１つの角ＢＡＣが角ＥＤＦに等しく、
　もう一つの角ＡＢＣ、ＤＥＦをはさむ辺が比例する、
　すなわち
　ＡＢがＢＣに対するように、
　ＤＥがＥＦに対し、
　残りのＣ、Ｆにおける角の双方が
　まず
　直角より小さい２つの三角形とせよ。

２辺が比例し、挟角以外が等しい三角形の作図は
下のようになる。
（以下、命題６ー７の補足 （作図.２辺が比例、挟角以外が等しい三角形）という。）
△ＡＢＣとＤＥについて
　命題１ー２３（作図・直線上に指定された角）
により
　半直線ＤＫ[;;∠ＥＤＫ＝∠ＢＡＣ]
をつくる。
　命題６ー２の補足（作図.比例第４項）、
　命題１ー３の補足（作図.等しい線分となる点）
により
　点Ｌ(ＤＫ;;ＢＡ：ＡＣ＝ＥＤ：ＤＬ)
をとる。
公準１ー１（作図.直線）
により
　ＥとＬを結ぶと、
　命題６ー６（２辺が比例し挟角が等しい三角形は等角）
により、
　△ＡＢＣ;(等角)△ＤＥＬ、
　ＡＢ：ＢＣ＝ＤＥ：ＥＬ
となっている。
命題の設定により、
　ＡＢ：ＢＣ＝ＤＥ：ＥＦ
となっているから、

　命題５ー１１（同一の比に同じ比）
により、
　ＤＥ：ＥＬ＝ＤＥ：ＥＦ
となり、
　命題５ー９（同一比の量）
により、
　ＥＬ＝ＥＦ
となっている。

よって
　公準１ー３（作図.円）
により、
　円(Ｅ,ＥＬ)
をとると、
　共有点(直線ＤＫ,円(Ｅ,ＥＬ));存在
となる。
　命題３ー１８の補足２(円と直線の共有点は２以下) により、
　共有点について、
　１つの場合、
　２つの場合
がある。
まず、
　１つの場合、
　命題３ー１８の補足２(円と直線の共有点は２以下)
により、
　直線ＤＫ(接)円(Ｅ,ＥＬ))
となり、
　Ｌ(すなわちＦ)以外に共有点はなく、
　Ｆ;＝Ｌ
として、
　△ＤＥＦ;＝△ＤＥＬ
をとる。
命題３－１６の系（系．接線は直径と直角）
により、
　∠ＥＦＤ＝∠Ｒ
となる。　
　２つの場合、
　命題３ー１８の補足２(円と直線の共有点は２以下)
により、
　ＤＫ(交)円(Ｅ,ＥＬ)、
　その交点は２つ
となり、
　もう１点をＬ'
とする。
　定義１ー４の補足２（同じ側・反対側(直線)）
により、
　直線ＤＫにおいて、
　Ｌ'がＤについてＬと同じ側の場合、
　Ｌ'がＤについてＬと反対側の場合
がある。
まず、
　Ｌ'がＤについてＬと同じ側の場合、
　Ｌ';上.半直線ＤＫ
となり、
　∠ＥＤＬ'＝∠ＢＡＣ
となり、
　Ｆ;＝ＬまたはＬ'
として、
　△ＤＥＦ;＝△ＤＥＬまたは△ＤＥＬ'
をとる。
　∠ＥＬＤ、∠ＥＬ'Ｄは、
　命題１ー５（２等辺三角形の底角）
　命題１ー３２（三角形の内対角・内角の和）
により、
　一方は鋭角であり、
　命題１ー１３（直線と２直角１）
　公理１ー３（等しいものから等しいものをひく）
により、
　他方は、鈍角である。
　Ｌ'がＤについてＬと反対側の場合、
　Ｌ';外.半直線
となり、
　Ｆ;＝Ｌのみ
として、
　△ＤＥＦ;＝△ＤＥＬ
をとる。
　∠ＥＦＤは、
　命題１ー５（２等辺三角形の底角）
　命題１ー３２（三角形の内対角・内角の和）
により、
　一方は鋭角である。
以上の２つの場合から、
　△ＡＢＣに
　２辺が比例、挟角以外が等しい△ＤＥＦが
　作図できる。
よって、
以上の２つの場合から、
　２辺が比例、挟角以外が等しい三角形
が作図できる。
　△ＡＢＣと線分ＤＥ
に対して、
　半直線ＤＫ[;;∠ＥＤＫ＝∠ＢＡＣ]
　点Ｌ(ＤＫ;;ＢＡ：ＡＣ＝ＥＤ：ＤＬ)
　交点Ｆ[半直線ＤＫ,円(Ｅ,ＥＬ)]
をとると、
　円(Ｅ,ＥＬ)(接)直線ＤＫ
ならば、
　△ＡＢＣ;∠Ｃ＝∠Ｒ、
　△ＤＥＦ;∠Ａ＝∠Ｄ、
　　ＡＢ：ＢＣ＝ＤＥ：ＥＦ、∠Ｆ＝∠Ｒ
となり、
　円(Ｅ,ＥＬ)(交)直線ＤＫ、
　交点Ｌ'(円(Ｅ,ＥＬ),直線ＤＫ;;外.Ｌ)
ならば、
　Ｌ';同側(ＤＫ,Ｄ,Ｌ)、上.ＤＬ
のとき
　Ｆ;＝Ｌ
とすると、
　△ＡＢＣ;∠Ｃ＜∠Ｒ、
　△ＤＥＦ;∠Ａ＝∠Ｄ、
　　ＡＢ：ＢＣ＝ＤＥ：ＥＦ、∠Ｆ＜∠Ｒ
となり、
　Ｆ;＝Ｌ'
とすると、
　△ＡＢＣ;∠Ｃ＜∠Ｒ、
　△ＤＥＦ;∠Ａ＝∠Ｄ、
　　ＡＢ：ＢＣ＝ＤＥ：ＥＦ、∠Ｆ＞∠Ｒ
となり、
　Ｌ';同側(ＤＫ,Ｄ,Ｌ)、延長.ＤＬ
のとき
　Ｆ;＝Ｌ
とすると、
　△ＡＢＣ;∠Ｃ＞∠Ｒ、
　△ＤＥＦ;∠Ａ＝∠Ｄ、
　　ＡＢ：ＢＣ＝ＤＥ：ＥＦ、∠Ｆ＞∠Ｒ
となり、
　Ｆ;＝Ｌ'
とすると、
　△ＡＢＣ;∠Ｃ＞∠Ｒ、
　△ＤＥＦ;∠Ａ＝∠Ｄ、
　　ＡＢ：ＢＣ＝ＤＥ：ＥＦ、∠Ｆ＜∠Ｒ
となり、
　Ｌ';反対側(ＤＫ,Ｄ,Ｌ)
のとき
　Ｆ;＝Ｌ
とすると、
　△ＡＢＣ;∠Ｃ＜∠Ｒ、
　△ＤＥＦ;∠Ａ＝∠Ｄ、
　　ＡＢ：ＢＣ＝ＤＥ：ＥＦ、∠Ｆ＜∠Ｒ
となる。
　△ＡＢＣ[;;∠Ｃ＜∠Ｒ]、ＤＥ
に対して、
上の補足により、
　△ＤＥＦ[ＡＢ：ＢＣ＝ＤＥ：ＥＦ,∠ＢＡＣ＝∠ＥＤＦ;;∠Ｆ＜∠Ｒ]
をとることができる。

三角形ＡＢＣは
　三角形ＤＥＦに等角であり、
　角ＡＢＣは角ＤＥＦに等しく、
　残りのＣにおける角は
　明らかに
　残りのＦにおける角に等しい
　と主張する。

もし
　角ＡＢＣが
　角ＤＥＦに等しくないならば、

背理法の仮定である。

　それらの一方は大きい。

公理１ー７の補足（線分・角は大か等か小）
による。
　∠ＡＢＣ＜＞∠ＤＥＦ
となっている。

角ＡＢＣが大きいとせよ。

角ＡＢＣが小さかったならば、
　記号を付け替えて、
　大きい方を三角形ＡＢＣとする。
　∠ＡＢＣ＞∠ＤＥＦ
としている。

そして
　線分ＡＢ上に
　その上の点Ｂにおいて
　ＤＥＦに等しい角ＡＢＧがつくられた
　とせよ。

命題１ー２３（作図・直線上に指定された角）
による。
　角ＡＢＧは角ＡＢＣより小さいので、
　公理１ー８の補足（小さい）
により、
　半直線ＡＧは角ＡＢＣの内部にある。
命題１ー２１の補足(三角形の角の分割線は対辺と交わる)
により、
　辺ＡＣと交わる。
　その交点を改めてＧとし、
　溯って用いている。
　∠ＡＢＧ＝∠ＤＥＦ
となっている。

そうすれば
　角Ａは角Ｄに、

命題の設定 による。
　∠Ａ＝∠Ｄ
となっている。

　角ＡＢＧは角ＤＥＦに等しいから、
　残りの角ＡＧＢは残りの角ＤＦＥに等しい。 【・・・(1)】

命題６ー５の補足（２組の角が等しい三角形は他の角も等しい）
による。
　∠ＡＧＢ＝∠ＤＦＥ
となっている。

それゆえ
　三角形ＡＢＧは三角形ＤＥＦに等角である。

定義の補足（命題４ー２）(等角)
による。
　△ＡＢＧ(等角)△ＤＥＦ
となっている。

ゆえに
　ＡＢがＢＧに対するように、
　ＤＥがＥＦに対する。

命題６ー４（等角三角形の等角辺の比例）
による。
　ＡＢ：ＢＧ＝ＤＥ：ＥＦ
となっている。

ところが
　ＤＥがＥＦに対するように、
　ＡＢがＢＣに対する
　と仮定されている。

命題の設定 による。
　ＤＥ：ＥＦ＝ＡＢ：ＢＣ
となっている。

したがって
　ＡＢは
　ＢＣ、ＢＨの双方に対し同じ比をもつ。

命題５ー１１（同一の比に同じ比）
による。
　ＡＢ：ＢＣ＝ＡＢ：ＢＨ
となっている。

それゆえ
　ＢＣがＢＧに等しい。

命題５ー９（同一比の量）
による。
　ＢＣ＝ＢＧ
となっている。

ゆえに
　Ｃにおける角は角ＢＧＣに等しい。

命題１ー４（２辺挟角相等）
による。
　∠Ｃ＝∠ＢＧＣ
となっている。

ところが
　Ｃにおける角は直角より小さい
　と仮定されている。

命題の設定 による。
　∠Ｃ＜∠Ｒ
となっている。

したがって
　角ＢＧＣも直角より小さい。

公理１ー８の補足２（等より大・小、大・小に等）
による。
　∠ＢＧＣ＜∠Ｒ
となっている。

それゆえ
　その接角ＡＧＢは直角より大きい。

定義１ー１０の補足（接角）、
命題１ー１３（直線と２直角１）、
公理１ー４の補足４（和が等しく一方が大きい）
による。
　∠ＡＧＢ＞∠Ｒ
となっている。

しかも
　Ｆにおける角に等しい
　ことが先に証明された。

(1) による。
　∠ＡＧＢ＝∠Ｆ
となっている。

ゆえに
　Ｆにおける角も直角より大きい
　ことになる。

公理１ー７（等しい）
による。
　∠Ｆ＞∠Ｒ
となっている。

ところが
　直角より小さい
　と仮定されている。

命題の設定による。
　∠Ｆ＜∠Ｒ
となっていた。

これは不合理である。

不合理であるという表現は初めてである。

したがって
　角ＡＢＣは角ＤＥＦに不等ではない。

背理法による。

それゆえ
　等しい。

　∠ＡＢＣ＝∠ＤＥＦ
となる。

ところが
　Ａにおける角もＤにおける角に等しい。

命題の設定による。
　∠Ａ＝∠Ｄ
となっている。

ゆえに
　残りのＣにおける角も
　残りのＦにおける角に等しい。

命題６ー５の補足（２組の角が等しい三角形は他の角も等しい）
による。
　∠Ｃ＝∠Ｆ
となる。

したがって
　三角形ＡＢＣは三角形ＤＥＦに等角である。

定義の補足（命題４ー２）(等角)
による。
　△ＡＢＣ(等角)△ＤＥＦ
となっている。

次に
　Ｃ、Ｆにおける角の双方が直角より小さくない
　と仮定されるとせよ。

　△ＡＢＣ[;;∠Ｃ＞＝∠Ｒ]、ＤＥ
に対して、
上の補足により、
　△ＤＥＦ[ＡＢ：ＢＣ＝ＤＥ：ＥＦ,
　　∠ＢＡＣ＝∠ＥＤＦ;;∠Ｆ＞＝∠Ｒ]
をとることができる。

このときにもまた
　三角形ＡＢＣは
　三角形ＤＥＦに等角である
　と主張する。
　
同じ作図がなされたとき、
　同様にして

背理法の仮定も含めて
　同様にしている。

　ＢＣがＢＧに等しい
　ことを証明しうる。

　ＢＣ＝ＢＧ
となっている。

それゆえ
　Ｃにおける角も角ＢＧＣに等しい。 【・・・(2)】

命題１ー５（２等辺三角形の底角）
による。
　∠Ｃ＝∠ＢＧＣ
となっている。

ところが
　Ｃにおける角は直角より小さくない。

命題の設定による。
　∠Ｃ＞＝∠Ｒ
となっている。

ゆえに
　角ＢＧＣも直角より小さくない。

公理１ー８の補足２（等より大・小、大・小に等）
による。
　∠ＢＧＣ＞＝∠Ｒ
となっている。

そこで
　三角形ＢＧＣの２角の和が
　２直角より小さくない
　ことになる。

公理１ー４の補足３（大きい（小さい）ものどうしを加える）
による。
　二等辺三角形ＢＧＣ
において、
　∠Ｃ＋∠ＢＧＣ＞＝２∠Ｒ
となっている。

これは不可能である。

命題１ー３２（三角形の内対角・内角の和）
による。

したがってまた
　角ＡＢＣはＤＥＦに不等ではない。

背理法による。

それゆえ
　等しい。

　∠ＡＢＣ＝∠ＤＥＦ
となっている。

ところが
　Ａにおける角もＤにおける角に等しい。

命題の設定による。
　∠Ａ＝∠Ｄ
となっている。

ゆえに
　残りのＣにおける角は
　残りのＦにおける角に等しい。

命題６ー５の補足（２組の角が等しい三角形は他の角も等しい）
による。
　∠Ｃ＝∠Ｆ
となっている。

したがって
　三角形ＡＢＣは三角形ＤＥＦに等角である。

定義の補足（命題４ー２）(等角)
による。

　△ＡＢＣ(等角)△ＤＥＦ
となっている。

よってもし
　２つの三角形が
　１つの角が互いに等しく、
　もう一つの角をはさむ辺が比例し、
　残りの角の双方が
　共に直角より小さいか、
　または
　共に小さくないならば、
　２つの三角形は等角であり、
　比例する２辺にはさまれる角は等しいであろう。
これが証明すべきことであった。

命題６ー７は、
　△ＡＢＣ[;;∠Ｃ＜∠Ｒ]
に対して、
　△ＤＥＦ[ＡＢ：ＢＣ＝ＤＥ：ＥＦ,
　　∠ＢＡＣ＝∠ＥＤＦ;;∠Ｆ＜∠Ｒ]、
　△ＡＢＣ[;;∠Ｃ＞＝∠Ｒ]
に対して、
　△ＤＥＦ[ＡＢ：ＢＣ＝ＤＥ：ＥＦ,
　　∠ＢＡＣ＝∠ＥＤＦ;;∠Ｆ＞＝∠Ｒ]、
をとれば、
　△ＡＢＣ(等角)△ＤＥＦ
のことである。
命題６ー７の補足（作図.２辺が比例、挟角以外が等しい三角形）

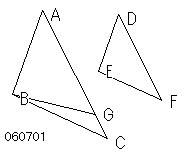
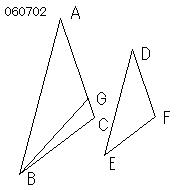
前提作図推論
定義 1-4系2
公準 1-1,1-3
公理 1-3
命題 1-3補,1-23,6-2補 1-5,1-13,1-32,3-16系,3-18補2,5-9,5-11,6-6
その他２段階の場合分け

命題６ー７は推論用命題である。

前提	作図	推論
定義		1-4補2,1-10,1-10補,補(題4-2)
公準	1-1,1-3
公理		1-3,1-4補3,1-4補4,1-7,1-7補,1-8補,1-8補2
命題	1-3補,1-21補,1-23,6-2補	1-5,1-13,1-32,3-16系,3-18補2,5-9,5-11,6-4,6-5補,6-6
その他		背理法,不合理

前　　次　　目次　　頁頭