ユークリッド原論をどう読むか（１）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論
第１巻

命題１ー５（２等辺三角形の底角）
　二等辺三角形の
　底辺の上にある角は
　互いに等しく、
　等しい辺が延長される
とき、
　底辺の下の角は
　互いに等しい
であろう。

• 　二等辺三角形は定義１ー２０による。
• 　底辺は定義１ー２０の補足２による。
• 　角は定義１ー８による。
• 　等しいは公理１ー７による。
• 　辺は定義１ー１９の補足による。

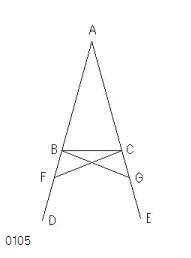
　ＡＢＣを
　辺ＡＢが辺ＡＣに
　等しい二等辺三角形
とし、
　線分ＢＤ、ＣＥが
　ＡＢ、ＡＣと一直線をなして
　延長された
とせよ。

• 　線分ＡＢ、
  　点Ｃ'[外.線分ＡＢ]、
  　点Ｃ(半直ＡＣ';;ＡＣ＝ＡＢ)、
  　線分ＢＣ、
  　点Ｄ[延長ＡＢ]、
  　点Ｅ[延長ＡＣ]
  をとる。
  

　角ＡＢＣは角ＡＣＢに、
　角ＣＢＤは角ＢＣＥに等しい
と主張する。

　ＢＤ上に任意の点Ｆがとられ、

• 公準１ー１の補足（作図.任意の点をとる）
  による。
• 　点Ｆ[ＢＤ]
  をとっている。

　大きい線分ＡＥから
　小さい線分ＡＦに
　等しいＡＧが切り取られ、 　　　　　　【・・・(a)】

• 命題１ー３（作図・等しい線分を切り取る）
  による。
• 命題１ー３（作図・等しい線分を切り取る）
  は
  　実質的には線分上に点をとることを
  　保証する命題である。
• 　点Ｇ(ＡＥ;;ＡＧ＝ＡＦ)
  をとっている。

　線分ＦＣ、ＧＢが結ばれた
とせよ。

• 　公準１ー１（作図.直線）
  による。
• 　線分(Ｆ,Ｃ)、線分(Ｇ,Ｂ)
  をとる。

そうすれば

　ＡＦはＡＧに、
　ＡＢはＡＣに等しい

• 　(a) ,命題の設定 による。
• 　ＡＦ＝ＡＧ、
  　ＡＢ＝ＡＣ
  となっている。

から、
　２辺ＦＡ、ＡＣは
　２辺ＧＡ、ＡＢにそれぞれ等しい。

• 　三角形の２辺を指示する
  とき、
  原論では
  　ＦＡ、ＡＣのように、
  　共通な頂点が真ん中にくる
  ように表現している。
• 　(ＦＡ,ＡＣ)＝(ＧＡ,ＡＢ)
  となっている。

そして
　共通の角ＦＡＧをはさむ。

• 　(a) による。
• 　∠ＦＡＧ;共通
  となっている。

それゆえ
　底辺ＦＣは
　底辺ＧＢに等しく、
　三角形ＡＦＣは
　三角形ＡＧＢに等しく、
　残りの角は
　残りの角に、
　等しい辺が対する角は
　等しくなる、

• 命題１ー４（２辺挟角相等）
  のことである。
• 　ＦＣ＝ＧＢ、
  　△ＡＦＣ≡△ＡＧＢ
  となっている。

すなわち
　角ＡＣＦは角ＡＧＢに、
　角ＡＦＣは角ＡＧＢに等しい
であろう。
　　　　　　【・・・(1)】

• 　前節の結果による。
• 　∠ＡＣＦ＝∠ＡＢＧ、
  　∠ＡＦＣ＝∠ＡＧＢ
  となっている。

そして
　ＡＦ全体はＡＧ全体に等しく、
　そのうち
　ＡＢはＡＣに等しい

• 　(a) ,命題の設定 による。
• 　ＡＦ＝ＡＧ、
  　ＡＢ＝ＡＣ
  となっている。

から、
　残りのＢＦは残りのＣＧに等しい
。

• 　公理１ー３による。
• 　ＢＦ＝ＣＧ
  となっている。

ところが
　ＦＣがＧＢに等しい
ことも先に証明された。

• 　(1) のことである。
• 　ＦＣ＝ＧＢ
  となっている。

かくて
　２辺ＢＦ、ＦＣは
　２辺ＣＧ、ＧＢにそれぞれ等しい。

• 　前節、前々節による。
• 　(ＢＦ,ＦＣ)＝(ＣＧ,ＧＢ)
  となっている。

しかも
　角ＢＦＣは角ＣＧＢに等しく、

• (1) による。
• 　∠ＢＦＣ＝∠ＣＧＢ
  となっている。

　≪底辺ＢＣはそれらに共通である。≫
それゆえ
　三角形ＢＦＣも三角形ＣＧＢに等しく、
　残りの角は残りの角に、
　すなわち
　等しい辺が対する角は
　それぞれ等しい
であろう。

• 　前節、前々節、命題１ー４（２辺挟角相等）
  による。
• 命題１ー４（２辺挟角相等）
  の成立に
  　「底辺ＢＣはそれらに共通である」は必要ない。
• 　△ＢＦＣ≡△ＣＧＢ
  となっている。

したがって
　角ＦＢＣは角ＧＣＢに、
　角ＢＣＦは角ＣＢＧに等しい。
　　　　　　【・・・(2)】

• 　前節による。
• 　∠ＦＢＣ＝∠ＧＣＢ、
  　∠ＢＣＦ＝∠ＣＢＧ
  となっている。

すると
　角ＡＢＧ全体が
　角ＡＣＦ全体に等しい
ことは先に証明されており、

• (1) による。
• 　平角ＡＢＦ、ＡＣＧ
  は、
  　原論において
  　角として認められていない
  ので、
  　∠ＡＢＧ、∠ＡＣＦ
  が注目されることになる。
• 　∠ＡＢＧ＝∠ＡＣＦ
  となっている。

そのうち
　角ＣＢＧは角ＢＣＦに等しい

• 　(2) による。
• 　∠ＣＢＧ＝∠ＢＣＦ
  となっている。

から、
　残りの角ＡＢＣは残りの角ＡＣＢに等しい。

• 　前節、前々節,公理１ー３（等しいものから等しいものをひく）
  による。
• 　∠ＡＢＣ＝∠ＡＣＢ
  となっている。

そして
　それらは
　三角形ＡＢＣの底辺の上にある。

• 　∠ＡＢＣ、∠ＡＣＢ
  　　;底辺ＢＣについて、
  　　　Ａと同じ側
  となっている。

また
　角ＦＢＣが角ＧＣＢに等しい
ことも先に証明された。
そして
　これらは底辺の下にある。

• (2) による。
• 　∠ＦＢＣ＝∠ＧＣＢ
  　∠ＦＢＣ、∠ＧＣＢ
  　　;底辺ＢＣについて、
  　　　Ａと反対側
  となっている。

よって
　二等辺三角形の底辺の上にある角は
　互いに等しく、
　等しい辺が延長される
とき、
　底辺の下の角は互いに等しい
であろう。

　これが証明すべきことであった。

• 　今日においては、
  　二等辺三角形ＡＢＣをひっくりかえし、
  　三角形ＡＢＣと三角形ＡＣＢが合同であることを
  　二角挟辺相等で証明する
  　ことも多い。
  　この方が補助線を必要とせず、
  　簡明である
  が、
  　原論としては
  　ひっくりかえすという方法を
  　できるだけ用いたくなかった
  ものと見られる。
  　原論の公理論的志向の現れ
  と見ることができる。
• 　点Ｆ、Ｇをとって、
  　三角形ＡＦＣ、ＡＢＧをつくるのは、
  　ひっくり返すということを
  　実質的にに行っている
  と見ることもできる。
  
  なお、
  　Ｆ、Ｇを
  　辺ＡＢ、ＡＣ上にとることは、
  　原論第一巻の論証過程においては、
  　証明完了までに至らない。
  
  　底辺の外角に注目することは
  　必然である。
• 　蛇足ながら、
  　この命題は、
  　俗にロバの橋と呼ばれている
  ものである。
  　循環論を
  　ユークリッドがどのように回避したか、
  　味わったいただくことになる。
• 命題1-5は、
  　△ＡＢＣ
  について、
  　ＡＢ＝ＡＣ、
  　点Ｄ(延長ＡＤ)
  　点Ｅ(延長ＡＥ)
  をとると、
  　∠ＡＢＣ＝∠ＡＣＢ、
  　∠ＣＢＤ＝∠ＢＣＥ
  のことである。
  
• 命題1-5は推論用命題である。

  前提	作図	推論
  定義
  公準	1-1、1-1補
  公理		1-3
  命題	1-3	1-4
  その他

前 　　 次 　　 目次 　　頁頭