ユークリッド原論をどう読むか（２）
頁末 　　 前 　　 次 　　 目次　

ユークリッド原論
第１巻

命題１ー２１（三角形の２辺の和と２線分の和）
(三角形の角の分割線は対辺と交わる。)

もし
　三角形の辺の一つの上に
　その両端から
　三角形の内部で交わる２線分が
　つくられる
ならば、
　つくられた２線分は
　その和が
　三角形の残りの２辺の和より小さいが、
　より大きい角をはさむ
であろう。

• 　三角形は、定義１ー１９の補足２による。
• 　辺は、定義１ー１９の補足による。
• 　線分は、定義１ー４の補足による。
• 　小さいは、公理１ー８の補足による。
• 　大きいは、公理１ー８による。
• 　角は、定義１ー９の補足による。

　三角形ＡＢＣの辺の一つＢＣの上に
　両端Ｂ、Ｃから
　三角形の内部で交わる
　２線分ＢＤ、ＤＣが
　つくられた
とせよ。

• 　△ＡＢＣ、
  　点Ｄ[△ＡＢＣ内]、
  　線分(Ｂ,Ｄ)、
  　線分(Ｃ,Ｄ)
  をとっている。

　ＢＤ、ＤＣは
　その和が
　三角形の残りの２辺ＢＡ、ＡＣの和より小さいが、
　角ＢＡＣより大きい角ＢＤＣを
　はさむ
と主張する。


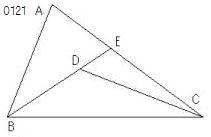
　ＢＤがＥまで延長された
とせよ。

• 　公準１ー２（作図.直線の延長）
  により延長され、
  　命題の補足３（定義１ー１４）（図形と直線の交点）
  により
  　少なくとも２点で交わる。
  　そのうち
  　１点は
  　辺ＡＢ、ＢＣの交点Ｂである
  から、
  　他の１点は
  　ＡＢ、ＢＣ上にはなく、
  　ＣＡ上にある
  から、
  　ＢＤ、ＣＡが交わる。
  　その交点をＥ
  とする。
• 　交点Ｅ(ＡＣ,ＢＤ)、
  　線分(Ｄ,Ｅ)
  をとっている。

そうすれば、
　すべての三角形において
　２辺の和は残りの１辺より大きい

• 　命題１ー２０（三角形の２辺の和と１辺）
  のことである。

から、
　三角形ＡＢＥの２辺ＡＢ、ＡＥの和は
　ＢＥより大きい。

• 　前節による。
• 　ＡＢ＋ＡＥ＞ＢＥ
  となっている。

　双方に
　ＥＣが加えられたとせよ。
そうすれば
　ＢＡ、ＡＣの和は
　ＢＥ、ＥＣの和より大きい。
　　　　　　【・・・(1)】

• 　公理１ー４（不等なものに等しいものを加える）
  による。
• 　ＢＡ＋ＡＣ＞ＢＥ＋ＥＣ
  となっている。

また
　三角形ＣＥＤの２辺ＣＥ、ＥＤの和は
　ＣＤより大きい

• 　命題１ー２０（三角形の２辺の和と１辺）
  による。
• 　ＣＥ＋ＥＤ＞ＣＤ
  となっている。

から、
　双方に
　ＢＤが加えられた
とせよ。
そうすれば
　ＣＥ、ＥＢの和は
　ＣＤ、ＤＢの和より大きい。
　　　　　　【・・・(2)】

• 　公理１ー４（不等なものに等しいものを加える）
  による。
• 　ＣＥ＋ＥＢ＞ＣＤ＋ＤＢ
  となっている。

ところが
　ＢＡ、ＡＣの和が
　ＢＥ、ＥＣの和より
　大きい
ことは先に証明された。

• 　(1) による。
• 　ＢＡ＋ＡＣ＞ＢＥ＋ＥＣ
  となっている。

したがって
　なおさらＢＡ、ＡＣの和は
　ＢＤ、ＤＣの和より大きい。

• 　(2) ,
  　公理１ー８の補足３（大きい・小さいものより大きい・小さい）
  による。
• 　ＢＡ＋ＡＣ＞ＢＤ＋ＤＣ
  となっている。

また、
　すべての三角形において
　外角は内対角より大きい

• 　命題１ー１６（外角と内対角）
  のことである。

から、
　三角形ＣＤＥの外角ＢＤＣは
　角ＣＥＤより大きい。
　　　　　　【・・・(3)】

• 　前節による。
• 　∠ＢＤＣ＞∠ＣＥＤ
  となっている。

それゆえ
　同じ理由で
　三角形ＡＢＥの外角ＣＥＢも
　角ＢＡＣより大きい。
　　　　　　【・・・(4)】

• 　命題１ー１６（外角と内対角）
  による。
• 　∠ＣＥＢ＞∠ＢＡＣ
  となっている。

ところが
　角ＢＤＣが
　角ＣＥＢより大きい
ことは先に証明された。

• 　(3) による。
• 　∠ＢＤＣ＞∠ＣＥＢ
  となっている。

したがって
　なおさら
　角ＢＤＣは角ＢＡＣより大きい。

• 　(4) ,
  　公理１ー８の補足３（大きい・小さいものより大きい・小さい）
  による。
• 　∠ＢＤＣ＞∠ＢＡＣ
  となっている。

よって
　もし三角形の辺の一つの上に
　その両端から三角形の内部で交わる
　２線分がつくられる
ならば、
　つくられた２線分は
　その和が三角形の残りの２辺の和より小さい
が、
　より大きい角をはさむ。
　
　これが証明すべきことであった。

• 　三角形の角を
  　２つに分ける直線は、
  　その対辺と
  　１点で交わる。
  　（以下、命題１ー２１の補足(三角形の角の分割線は対辺と交わる) という。）
  　命題の補足３（定義１ー１４） （図形と直線の交点）
  により、
  　角（頂点）以外に
  　少なくとも１点で、
  　三角形の境界と交わる
  が、
  　その角をなす２辺とは交わらない。
  　背理法の仮定として
  もし
  　交わる
  なら、
  　公理１ー９ （２点を通る直線は一致）
  により、
  　その辺と直線は一致する
  から、
  　角を２つに分けない。
  　これは設定に反する。
  したがって
  　背理法により
  　その角をなす２辺とは交わらない。
  よって、
  　対辺と交わる。
  対辺は、
  　その角を通らない
  から、
  　角を２つに分ける直線とは
  　異なる直線である。
  したがって、
  　交点は１つである。
• 命題1-21は、
  　△ＡＢＣ
  に対して、
  　点Ｄ[△ＡＢＣ内]、
  　線分(Ｂ,Ｄ)、
  　線分(Ｃ,Ｄ)
  ならば、
  　ＢＤ＋ＤＣ＜ＢＡ＋ＡＣ
  　∠ＢＤＣ＞∠ＢＡＣ
  のことである。
• 命題の補足３（定義１ー１４）（図形と直線の交点）

  前提	作図	推論
  定義
  公準
  公理		1-9
  命題		補3(義1-14)
  その他		背理法

• 命題1-21は推論用命題である。

  前提	作図	推論
  定義
  公準	1-2
  公理		1-4、1-8補3
  命題	補3(義1-14)	1-16、1-20
  その他

前 　　 次 　　 目次 　　頁頭