ユークリッド原論をどう読むか(2)
頁末
前
次
目次
ユークリッド原論
第1巻
命題1ー13(直線と2直角1)
もし
直線が直線の上に立てられて
二つの角をつくる
ならば、
二つの直角か
または
その和が2直角に等しい角を
つくる
であろう。
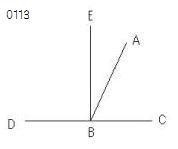
任意の直線ABが
直線CD上に立てられて
角CBA、ABDをつくる
とせよ。
-
直線(C,D)、
点B[CD]、
点A[外.CD]、
直線(A,B)
をとっている。
角CBA、ABDは
二つの直角であるか
または
その和が2直角に等しい
と主張する。
さて
[等しい場合]
もし
角CBAが
角ABDに等しけれ
ば、
それらは二つの直角である。
-
定義1ー10(直角)
による。
-
∠CBA=∠ABD=∠R
となっている。
[一方が他方より小さい場合]
だが
もし
等しくなけれ
ば、
[小さい方を角CBAと置き換えて]
点BからCDに
直角にBEがひかれた
とせよ。
【・・・(a)】
-
命題1ー11(作図・線分からの垂線)
による。
-
点E[外.CD;;EB⊥CD]
をとっている。
すると
角CBE、EBDは二つの直角である。
そして
角CBEは
2角CBA、ABEの和に等しい。
-
(a)
により、
角CBAは
直角より小さい
ことによる。
-
∠CBE+∠EBD=2×∠R、
∠CBE=∠CBA+∠ABE
となっている。
双方に
角EBDが加えられた
とせよ。
そうすれば
角CBE、EBDの和は
3角CBA、ABE、EBDの和に等しい。
【・・・(1)】
-
公理1ー2(等しいものに等しいものを加える)
による。
-
∠CBE+∠EBD
=∠CBA+∠ABE+∠EBD
となっている。
また
DBAは
2角DBE、EBAの和に等しい
から、
双方に角ABCが加えられた
とせよ。
そうすれば
角DBA、ABCの和は
3角DBE、EBA、ABCの和に等しい。
【・・・(2)】
-
公理1ー2(等しいものに等しいものを加える)
による。
-
∠DBA+∠ABC
=∠DBE+∠EBA+∠ABC
となっている。
ところが
角CBE、EBDの和が
この同じ三つの角に等しい
ことも先に証明された。
そして
同じものに等しいものは
また
互いに等しい。
それゆえ
角CBE、EBDの和は
角DBA、ABCの和に等しい。
【・・・(3)】
-
(1)
(2)
,
公理1ー1(同じものに等しい)
による。
-
∠CBE+∠EBD
=∠DBA+∠ABC
となっている。
ところが
角CBE、EBDは二つの直角である。
-
(a)
による。
-
∠CBE+∠EBD=2×∠R
となっている。
ゆえに
角DBA、ABCの和は
2直角に等しい。
-
(3)
による。
-
今日でいうところの平角CBDは、
原論では角として認められていない。
2直角という値をもつ角ではない。
したがって、
角CBEとEBDの和と
角CBA、ABEとEBDの和と
角DBAとABCの和が
一致していて、
角CBEとEBDが
それぞれ直角である
ことから
角DBAとABCの和が2直角である
と推論されているのである。
つまり、
平角CBDと
角DBAとABCの和とが
図形の角として
互いに重なり合っているという論法は
使えない
としている。
-
∠DBA+∠ABC=2×∠R
となっている。
[したがって、
2つの場合の結果により
角DBA、ABCは
2つの直角であるか
その和が2直角に等しい]
よって
もし直線が
直線の上に立てられて
二つの角をつくるならば、
二つの直角か
または
その和が2直角に等しい角をつくる
であろう。
これが証明すべきことであった。
- 命題1-13は、
CD;直線
に対して、
A;点[外.CD]、
B;点[CD]
ならば、
∠CBA、∠ABD;
∠CBA=∠ABD=直角
または、
∠CBA+∠ABD=2直角
のことである。
- 命題1-13は推論用命題である。
前
次
目次
頁頭
