ユークリッド原論をどう読むか（１）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論
第１巻

命題１ー４（２辺挟角相等）
「なぜならもし」
もし
　二つの三角形が
　２辺が２辺にそれぞれ等しく、
　その等しい２辺に
　はさまれる角が等しい
ならば、
　底辺は底辺に等しく、
　三角形は三角形に等しく、
　残りの２角は残りの２角に、
　すなわち
　等しい辺が対する角は
　それぞれ等しい
であろう。

• 　いわゆる二辺挟角相等の合同条件である。
• 　三角形は定義１ー１９の補足２による。
• 　辺は定義１ー１９の補足による。
• 　等しいは公理１ー７による。
• 　角は定義１ー８による。
• 　底辺は定義１ー２０の補足２による。

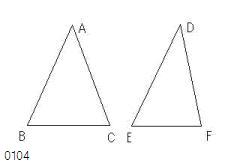
　ＡＢＣ、ＤＥＦを
　２辺ＡＢ、ＡＣが２辺ＤＥ、ＤＦに、
　すなわち
　ＡＢがＤＥに、ＡＣがＤＦに
　それぞれ等しく、
　かつ
　角ＢＡＣが角ＥＤＦに等しい
　二つの三角形
とせよ。

• 　△ＡＢＣ、△ＤＥＦ
  　；（ＡＢ＝ＤＥ、ＡＣ＝ＤＦ、
  　　　∠ＢＡＣ＝∠ＥＤＦ）
  となっている。
  

　底辺ＢＣは底辺ＥＦに等しく、
　三角形ＡＢＣは三角形ＤＥＦに等しく、
　残りの角は残りの角に、
　等しい辺が対する角はそれぞれ等しい、
　すなわち
　角ＡＢＣは角ＤＥＦに、
　角ＡＣＢは角ＤＦＥに等しい
であろうと主張する。

• 　この命題には、
  　補助線等を作図する部分がない。

　三角形ＡＢＣが三角形ＤＥＦに重ねられ、

• 　原論に特徴的な
  　動かして重ねる
  ことで論証する証明法である。
  　上に重ねて描く
  と
  　結局、重なるようにしか描けない
  　ことを論証している
  と見ることもできる。
  

　点Ａが点Ｄの上に、
　線分ＡＢがＤＥの上におかれれ
ば、

• 　定義１ー４により
  　おくことができる。
• 　上に重ねて写すという観点からは、
  　次のように読み替える。
  　点Ａ'を
  　Ｄに重ねてとり、
  　線分Ａ'Ｂ'を
  　半直線ＤＥに重ねてとる。
  
• 　Ａ≡Ｄ
  となっている。

　ＡＢはＤＥに等しい

• 　命題の設定による。
• 　ＡＢ＝ＤＥ
  となっている。

から、
　点ＢもＥに重なる
であろう。
　　　　　　【・・・(1)】

• 　公理１ー７による。
• 　重ね書きと見る場合には、
  　命題１ー３（作図・等しい線分を切り取る）　
  により、
  　半直線ＤＥ上に、
  　ＤＢ'＝ＡＢとなるように
  　Ｂ'をとる
  ならば、
  　ＤＥ＝ＡＢである
  から
  　Ｅ≡Ｂ'
  となっている。
  
• 　Ｂ≡Ｅ
  となっている。

また、
　ＡＢがＤＥに重なる
とき、
　角ＢＡＣが角ＥＤＦに等しい

• 　命題の設定による。
• 　∠ＢＡＣ＝∠ＥＤＦ
  となっている。

から、
　線分ＡＣもＤＦに重なる
であろう。

• 　前節、
  　公理１ー７による。
• 　重ね書きと見る場合には、
  　直線上に等しい角を描くのは、
  　命題１ー２３（作図・直線上に指定された角）
  によるから、
  　ここでは、
  　原理的に仮想的に
  　推論する
  ことになる。
  　ＡからＢを見て、
  　Ｃがある側に、
  　Ａ'からＢ'を見て、
  　Ｃ"がくるように、
  　角Ｂ'Ａ'Ｃ"を
  とる。
  　線分Ａ'Ｂ'(ＤＥ)について
  　Ｃ"が、
  　Ｆと同じ側か
  　異なる側か
  どちらかになる。
  　同じ側とする
  ならば、
  　∠ＢＡＣと∠ＥＤＦが等しい
  から、
  　公理１ー７（等しい）
  により
  　半直線Ａ'Ｃ"
  は
  　半直線ＤＦの上に重なってとられる。
  
  　異なる側とする
  ならば、
  　何も書かれていない所に
  　半直線Ａ'Ｃ"をとる。
  が、
  　公理１ー７（等しい）
  により、
  　この半直線Ａ'Ｃ"以外には書きえない。　
  
• 　半直線ＡＣ≡ＤＦ
  となっている。

それゆえ、
　ＡＣがまたＤＦに等しい

• 　命題の設定による。
• 　ＡＣ＝ＤＦ
  となっている。

から、
　点Ｃも点Ｆに重なる
であろう。
　　　　　　【・・・(2)】

• 　前節、前々節、
  　公理１ー７による。
• 　重ね書きと見るならば、
  　半直線Ａ'Ｃ'が
  　半直線ＤＦの上に重なってとられた
  ならば、
  　命題１ー３（作図・等しい線分を切り取る）　
  により
  　Ａ'Ｃ'＝ＡＣとなるように
  　Ｃ'をとると、
  　ＤＦ＝ＡＣであったから
  　Ｃ'≡Ｆとなる。
  
  　異なる側にかいて
  　何も書かれていない所に
  　半直線Ａ'Ｃ'をとった
  ならば、
  　命題１ー３（作図・等しい線分を切り取る）　
  により
  　この半直線上に
  　Ａ'Ｃ'＝ＡＣとなるように
  　Ｃ'をとると、
  　Ｃ'の位置はここ以外には
  　なりえない。
  
• 　Ｃ≡Ｆ
  となっている。

ところが
　点ＢもすでにＥと重なっている。

　
• (1)による。
• 　Ｂ≡Ｅ
  となっている。

したがって
　底辺ＢＣは底辺ＥＦに重なる
であろう。

なぜならもし、

• 　「なぜならもし(for if)」と、
  　背理法を伴って
  　根拠を後に述べるスタイルが、
  　ここに初めて登場する。
  原論では、
  　このスタイルはあまりない。
  　後世の注釈の混入
  と考えられている。
  　以下、コメント（命題１ー４）(なぜならもし)という。

　ＢがＥに、
　ＣがＦに重なっている
のに、

• 　(1) (2) による。
• 　Ｂ≡Ｅ、Ｃ≡Ｆ
  となっている。

　底辺ＢＣがＥＦに重ならない
ならば、

• 背理法の仮定である。
  原論では
  　ここに背理法が初めて登場する。
• 　ＢＣ¬≡ＥＦ
  となるならば
  ということである。

　２線分が面積を囲む
ことになるであろう。

• 　前節、前々節、
  　公理１ー９による。

　これは不可能である。
それゆえ
　底辺ＢＣはＥＦに重なり
　それに等しくなる
であろう。

• 背理法による。
  
• 　ＢＣ≡ＥＦ
  となっている。

したがって
　三角形ＡＢＣ全体も三角形ＤＥＦ全体に重なり
　それに等しくなる
であろう。

• 合同であるということである。
• 　重ね書きと見て、
  　∠ＢＡＣを
  　線分Ａ'Ｂ'(ＤＥ)について
  　同じ側に書いた
  とすれば、
  　ここまで
  　まったく同様である。
  
  　異なる側にかいて
  　何も書かれていない所に
  　半直線Ａ'Ｃ'をとった
  とすれば、
  　Ｃ'の位置はただ１点に限定された
  から
  　公準１ー１（作図.直線）
  により、
  　Ｂ'とＣ'を結ぶ
  ならば、
  　描かれる三角形はただ１つしかありえない。
  ここで、
  　この三角形を、
  　Ａ'Ｂ'を軸に折り返す
  と、
  　本命題の推論
  により、
  　２つの三角形がまったく重なる。
  
  
• 　△ＡＢＣ≡△ＤＥＦ
  となっている。

そして
　残りの角も残りの角に重なり
　それと等しくなる
であろう、
すなわち
　角ＡＢＣは角ＤＥＦに、
　角ＡＣＢは角ＤＦＥに等しくなる
であろう。

• 　今日であれば
  　合同であるといえば、
  　敢えてこの部分を述べることはしない。
  したがって、
  　合同という概念が確立しきっていない
  　と見ることができる。
• 　∠ＡＢＣ＝∠ＤＥＦ、
  　∠ＡＣＢ＝∠ＤＦＥ
  となっている。

よってもし
　２つの三角形が
　２辺が２辺にそれぞれ等しく、
　その等しい２辺に
　はさまれる角が等しい
ならば、
　底辺は底辺に等しく、
　三角形は三角形に等しく、
　残りの２角は残りの２角に、
　すなわち
　等しい辺が対する角は
　それぞれ等しい
であろう。

　これが証明すべきことであった。

• 　重ねて合わせることによって、
  あるいは、
  　重ねて上に描くことによって
  　証明している。
  
  　この証明法が
  　ここに原論で初めて登場している。
• 命題１ー３で、
  　直線は
  　どこにでも写せる
  　ことが確認できた。
  
  　直線が写せれ
  ば、
  　定義１ー１０により、
  　定義され
  　公準１ー４により、
  　確定される
  　直角を写すことが
  　理念的にしたがって仮想的にできる。
  したがって
  　角も写すことができる。
  と想定される。
  その結果、
  　重ねあわせが
  　原理的に可能である
  ことが、
  　命題１ー３までで確認されている
  とみることもできる。
  なお、
  　直角や等しい角が
  　現実的に作図できることは、
  　仮想的な論証を前提にして、
  後に、
  　命題１ー１１（作図・線分からの垂線）、
  　命題１ー２３（作図・直線上に指定された角）
  で示される。
  　
• 　いわゆる
  　裏返しの場合は明示的には
  　示されていない。
  
  　重ね書きと見ると、
  　ＡからＢを見て、
  　Ｃのある側に。
  　ＤからＥを見て、
  　Ｆがない場合、
  　最後に折り返すこと
  により、
  　本命題の推論を繰り返して、
  　全く重なる
  ことを論証する。
  　命題１ー３（作図・等しい線分を切り取る）
  を用いるなど、
  　手順が明確なだけ、
  　重ね書きと見る方がよい
  であろう。
  
• 　命題1-4は、
  　△ＡＢＣ、ＤＥＦ
  に対して、
  　ＡＢ＝ＤＥ、ＡＣ＝ＤＦ、
  　∠ＢＡＣ＝∠ＥＤＦ
  ならば、
  　△ＡＢＣ≡△ＤＥＦ
  のことである。
  
• 　命題1-4は原論最初の推論用命題である。

  前提	作図	推論
  定義	(1-10)	1-4
  公準	(1-4)
  公理		1-7、1-9
  命題	(1-3)
  その他		重ね合わせ、背理法、コ(題1-4)fi

前 　　 次 　　 目次 　　頁頭