ユークリッド原論をどう読むか（１０）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第６巻

命題６ー８（直角三角形の垂線と相似）
比例中項　 （系　直角三角形の垂線は比例中項）
（等角な三角形は相似）

もし
　直角三角形において
　直角から底辺に垂線がひかれるならば、
　垂線の上の三角形は
　全体に対し
　かつ
　互いに
　相似である。

• 直角三角形は、定義１ー２１ による。
• 直角は、定義１ー１０ による。
• 底辺は、定義１ー２０の補足２ による。
• 垂線は、定義１ー１０ による。
• 三角形は、定義１ー１９の補足２ による。
• 相似は、定義６ー１ による。

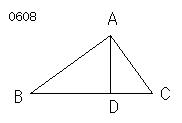
ＡＢＣを
　角ＢＡＣが直角である
　直角三角形とし、
　ＡからＢＣに
　垂線ＡＤが下されたとせよ。

• 命題１ー１２（作図・線分への垂線）
  による。
  命題１ー２１の補足(三角形の角の分割線は対辺と交わる)
  により、
  　辺ＢＣと交わる。
  その点をＤとし、
  　溯ってＤを用いている。
  
• 　△ＡＢＣ
  に対して、
  　Ｄ(ＢＣ;;ＡＤ⊥ＢＣ)
  をとっている。

三角形ＡＢＤ、ＡＤＣの双方は
　全体ＡＢＣに対し、
　また
　互いに
　相似である
　と主張する。
　
角ＢＡＣは角ＡＤＢに等しい、
　なぜなら
　どちらも直角であるから。

• 命題の設定 による。
• 　∠ＢＡＣ＝∠ＡＤＢ＝∠Ｒ
  となっている。

そして
　Ｂにおける角は
　２つの三角形ＡＢＣ、ＡＢＤに共通であるから、
　残りの角ＡＣＢは
　残りの角ＢＡＤに等しい。

• 命題６ー５の補足（２組の角が等しい三角形は他の角も等しい）
  による。
• 　∠Ｂ;共通、
  　∠ＡＣＢ＝∠ＢＡＤ
  となっている。

それゆえ
　 三角形ＡＢＣは
　三角形ＡＢＤに等角である。 【・・・(1)】

• 定義の補足（命題４ー２）(等角)
  による。
• 　△ＡＢＣ(等角)△ＡＢＤ
  となっている。

ゆえに
　三角形ＡＢＣの直角を張るＢＣが

• 角を張る辺
  　という表現が初めて登場する。
  これまでは
  　角に対する辺
  　と表現されていた。
  比例における
  　対するという表現と
  　区別するためであろう。
  なお、
  　英文では、
  　which is opposite the right angle　
  と
  　Ａ is to B, as C is to D
  と表現がそもそも区別されている。

　三角形ＡＢＤの直角を張るＢＡに対するように、
　三角形ＡＢＣのＣにおける角を張るＡＢそのものが
　三角形ＡＢＤの等しい角ＢＡＤを張るＢＤに対し、
　そしてまた
　ＡＣが
　２つの三角形に共通な
　　Ｂにおける角を張るＡＤに対する。

• 命題６ー４（等角三角形の等角辺の比例）
  による。
  
• 　ＢＣ：ＢＡ＝ＡＢ：ＢＤ＝ＡＣ：ＡＤ
  となっている。

したがって
　三角形ＡＢＣは
　三角形ＡＢＤに等角であり、
　等しい角をはさむ辺が比例する。

• 　△ＡＢＣ(等角)△ＡＢＤ
  となっている。

それゆえ
　三角形ＡＢＣは
　ＡＢＤに相似である。

• 定義６ー１（相似）
  による。
• したがって、
  　定義の補足（命題４ー２）(等角)
  　命題６ー４（等角三角形の等角辺の比例）
  　定義６ー１（相似）
  により、
  等角な三角形は相似な三角形である。
  （以下、命題６ー８の補足２ (等角な三角形は相似)という。）
• 　△ＡＢＣ∽△ＡＢＤ
  となっている。

同様にして、
　三角形ＡＢＣは
　三角形ＡＤＣに相似である
　ことを証明しうる。

• 　△ＡＢＣ∽△ＡＤＣ
  となっている。

ゆえに
　三角形ＡＢＤ、ＡＤＣの双方は
　全体ＡＢＣに相似である。

次に
　三角形ＡＢＤ、ＡＤＣが
　互いに相似である
　と主張する。
　
直角ＢＤＡは
　直角ＡＤＣに等しく、
　また
　角ＢＡＤもＣにおける角に等しい
　ことが証明されたから、

• (1) による。
• 　∠ＢＤＡ＝∠ＡＤＣ＝∠Ｒ、
  　∠ＢＡＤ＝∠Ｃ
  となっている。

　残りのＢにおける角も
　角ＤＡＣに等しい。

• 命題６ー５の補足（２組の角が等しい三角形は他の角も等しい）
  による。
• 　∠Ｂ＝∠ＤＡＣ
  となっている。

それゆえ
　三角形ＡＢＤは
　三角形ＡＤＣに等角である。

• 定義の補足（命題４ー２）(等角)
  による。
• 　△ＡＢＤ(等角)△ＡＤＣ
  となっている。

ゆえに
　三角形ＡＢＤの角ＢＡＤを張るＢＤが
　三角形ＡＤＣの、
　角ＢＡＤに等しい
　　Ｃにおける角を張るＤＡに対するように、
　三角形ＡＢＤの
　　Ｂにおける角を張るＡＤそのものが
　三角形ＡＤＣの、
　Ｂにおける角に等しい
　　角ＤＡＣを張るＤＣに対し、
　また
　共に直角を張るＢＡが
　ＡＣに対する。

• 命題６ー８の補足２(等角な三角形は相似)
  による。
• 　ＢＤ：ＤＡ＝ＡＤ：ＤＣ＝ＢＡ：ＡＣ
  となっている。

したがって
　三角形ＡＢＤは
　三角形ＡＤＣに相似である。

• 定義６ー１（相似）
  による。
• 　△ＡＢＤ∽△ＡＤＣ
  となっている。

よってもし
　直角三角形において
　直角から底辺に垂線がひかれるならば、
　垂線の上の三角形は
　全体に対し
　かつ
　互いに相似である。
　
系
これから
　次のことが明らかである、
　すなわち
　もし直角三角形において
　直角から底辺に垂線が下されるならば、
　下された垂線は
　底辺の２つの部分の比例中項である。
（以下、命題６ー８の系（直角三角形の垂線は比例中項）という。）

• 比例中項 とは、
  　ａがｂに対するように
  　ｂがｃに対するときの
  　ｂをいう。
  （以下、定義の補足３（命題６ー８） (比例中項)という。）
  単に中項 ともいう。
  （命題６ー１７ （比例３線分と外項矩形、中項正方形） を参照のこと）
  ａ、ｂ、ｃという
  　比例する列があって、
  　中央の項のことである。
  ある意味では、
  　等間隔比という発想と対応している。
• 　命題６ー８（直角三角形の垂線と相似）
  　命題６ー４（等角三角形の等角辺の比例）
  　定義の補足３（命題６ー８）(比例中項)
  による。
  
• 　△ＡＢＣ
  に対して、
  　Ｄ(ＢＣ;;ＡＤ⊥ＢＣ)
  をとれば、
  　ＢＤ：ＡＤ＝ＡＤ：ＤＣ
  となっている。

　
これが証明すべきことであった。

• 命題６ー８は、
  　△ＡＢＣ
  に対して、
  　Ｄ(ＢＣ;;ＡＤ⊥ＢＣ)
  をとれば、
  　△ＡＢＣ∽△ＡＢＤ、
  　△ＡＢＣ∽△ＡＤＣ、
  　△ＡＢＤ∽△ＡＤＣ
  のことである。
  
• 命題６ー８の系（直角三角形の垂線は比例中項）

  前提	作図	推論
  定義		補3(題6-8)
  公準
  公理
  命題		6-4,6-8
  その他

• 命題６ー８の補足２ (等角な三角形は相似)

  前提	作図	推論
  定義		補(題4-2),6-1
  公準
  公理
  命題		6-4
  その他

• 命題６ー８は推論用命題である。

  前提	作図	推論
  定義		補(題4-2),6-1
  公準
  公理
  命題	1-12,1-21補	6-4,6-5補,6-8補2
  その他

前 　　 次 　　 目次 　　頁頭