�ɂ��A
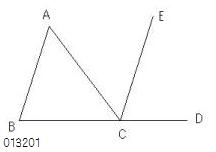
�@����P�[�R�P�i��}�E���s���j
�ɂ�����^��A�����������B
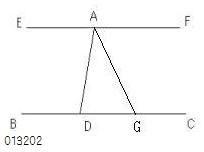
����P�[�R�O�i���s�̕��s�j
�ɂ��A
�@�����a�b�ɕ��s��
�@�_�`��ʂ�A
�@���p�a�c�`�Ƃe�`�c�������������d�e�������B
�����P�[�P�i��}.�����j
�ɂ��A
�@�����a�b��ɂ�����
�@�c�ƈقȂ�_�f�Ƃ����ԁB
���̂Ƃ��A
�@���p�a�f�`�Ƃe�`�f�Ƃ����������Ƃ�
�@���̂悤�Ɏ������Ƃ��ł���B
�@
����P�[�R�Q�i�O�p�`�̓��Ίp�E���p�̘a�j
�ɂ��A
�@�p�a�c�`��
�@���Ίp�c�`�f�Ƃc�f�`�̘a�ɓ������Ȃ�B
�����P�[�P�i�������̂ɓ������j
�ɂ��A
�@�p�e�`�c�͂c�`�f�Ƃc�f�`�̘a�ɓ������Ȃ�B
�����P�[�V�i�������j
�ɂ��A
�@�p�e�`�c�͂e�`�f�Ƃc�`�f�̘a�ɓ������Ȃ�B
�����P�[�R�i���������̂��瓙�������̂��Ђ��j
�ɂ��A
�@�p�c�f�`�Ƃe�`�f�͓������Ȃ�B
����āA
�@�p�a�f�`�Ƃe�`�f�Ƃ�������
����
�@�����P�[�T�i���s�������j
��
�@�ȉ��̂悤�ɓ������Ƃ��ł���B
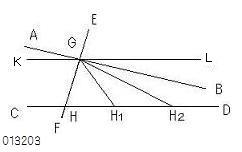
�Q�����`�a�A�b�c��
�@�����d�e��
�@���ꂼ��f�A�g�Ō�����Ă���A
�@�������p�a�f�g�Ƃf�g�c�̘a��
�@�Q���p��菬�������̂Ƃ���B
�@
����P�[�R�P�i��}�E���s���j
�i�����P�[�T�i���s�������j
��O��Ƃ��Ȃ��j
�ɂ��A
�@�f��ʂ�b�c�ɕ��s�Ȓ����j�k���A
�@���p�f�g�b�Ƃk�f�g���������Ȃ�悤�Ɉ����B
���̂Ƃ��A
�@�p�f�g�c�Ƃk�f�g�̘a��
�@�p�f�g�c�Ƃf�g�b�̘a�ɓ������A
�@��҂�
�@�Q���p�ł��邩��A
�@�����P�[�Q�i���������̂ɓ��������̂�������j
�ɂ��A
�@�p�f�g�c�Ƃk�f�g�̘a���Q���p�ł���B
�p�f�g�c�Ƃa�f�g�̘a��
�@�Q���p��菬�����̂ŁA
�@�����P�[�W�̕⑫�i�������j
�ɂ��A
�@�p�a�f�g�͂k�f�g��菬�����B
�����
�@�������f�a�͊p�k�f�g�̓����ɂ���B
����P�[�Q�i��}�E�����j
�ɂ��A
�@�������g�c��ɓ_�g1���A
�@�g�g1���g�f�Ɠ������Ȃ�悤�ɂƂ�A
�@�����P�[�P�i��}.�����j
�ɂ��f�Ƃg1�����ԁB
�O�p�`�g�f�g1��
�@�g�f�Ƃg�g1���������ӎO�p�`�ł��邩��A
�@����P�[�T�i�Q���ӎO�p�`�̒�p�j
�ɂ��A
�@�p�g�f�g1�Ƃg�g1�f�͓������B
�܂��A
�@����P�[�R�Q�i�O�p�`�̓��Ίp�E���p�̘a�j
�ɂ��A
�@�p�g�f�g1�Ƃg�g1�f�̘a�͊p�b�g�f�Ɠ������B
���s����������}�̐ݒ�ɂ��A
�@���p�b�g�f�Ƃk�f�g�͓������̂ŁA
�@�����P�[�P�i�������̂ɓ������j
�ɂ��A
�@�p�g�f�g1�Ƃg�g1�f�̘a�͊p�k�f�g�ɓ������B
�����P�[�R�i���������̂��瓙�������̂��Ђ��j
�ɂ��A
�@�p�k�f�g1�͊p�g�f�g1�Ɠ������Ȃ�̂ŁA
�@�����P�[�P�i�������̂ɓ������j
�ɂ��
�@�p�g�f�g1�Ƃk�f�g1�͓������A
�@�f�g1�͊p�k�f�g�̂Q�������ƂȂ��Ă���B
���ɁA
�@����P�[�Q�i��}�E�����j
�ɂ��A
�@�������g1�c��ɁA
�@�_�g2���g1�g2���g1�f�Ɠ������Ȃ�悤�ɂƂ�A
�@�����P�[�P�i��}.�����j
�ɂ��
�@�f�Ƃg1�����ԂƁA
�@�f�g2��
�@�p�k�f�g1�̂Q�������ƂȂ邱�Ƃ�
�@���l�ɂ��Ă킩��B
���������n��J��Ԃ��ƁA
�@�����P�[�Q�̕⑫�i�A���L���f�X�̌����j
�ɂ��
�@�b�c��ɓ_�gn�������āA
�@�p�k�f�gn�͊p�k�f�g��1/2n�ƂȂ�̂ŁA
�@�\���傫��m���Ƃ�Ɗp�k�f�gm��
�@�p�k�f�a��菬�����Ȃ�B
���̂Ƃ��A
�@�gm�͂b�c��ɂ���A
�@�����P�[�W�̕⑫�i�������j
�ɂ��A
�@�p�a�f�g�͂g�f�gm��菬�����Ȃ�̂ŁA
�@�������f�a�͊p�g�f�gm�̓����ɂ���B
����āA
�@��`�P�[�P�S�̕⑫�i�����(�}�`)�j
�ɂ��A
�@�f�a�͂b�c�ƌ�_�����B
���Ȃ킿
�@�����d�e�ɂ���
�@�������p���Q���p��菬��������
�@��_�����B
����������P�[�T�i���s�������j
����������B
�@����P�[�Q�X�i���s�ƍ��p�A���Ίp�A�������p�j�A
�@����P�[�R�O�i���s�̕��s�j�A
�@����P�[�R�O�̕⑫(����ɕ��s�Ȑ�) �A
�@����P�[�R�P�̕⑫(�^�_��ʂ镽�s���͗B��)�A
�@����P�[�R�Q�i�O�p�`�̓��Ίp�E���p�̘a�j
��
�@�����P�[�T�i���s�������j
�Ɠ��l�ł���B
�@�O�p�`�`�a�b
�ɂ����āA
�@�_�c[�����a�b]�A
�@�����b�c
���Ƃ�A
�@�ڂ`�b�c���ڂb�`�a�{�ڂ`�a�b�A
�@�ڂ`�a�b�{�ڂa�b�`�{�ڂb�`�a
�@���Q�ڂq
�̂��Ƃł���B
| �O�� | ��} | ���_ |
| ��` | ||
| ���� | 1-2�A1-2�� | |
| ���� | 1-1�A1-2 | |
| ���� | 1-31 | 1-13,1-29 |
| ���̑� |