ユークリッド原論をどう読むか（１０）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第６巻

命題６ー２３（等角な平行四辺形と辺の比の積）
（比の積は逆順でも同じ）
（小さい比との積は小さい）
等角な２つの平行四辺形は
　互いに辺の比の積の比をもつ。

• 等角は、 定義の補足（命題４ー２） による。
• 平行四辺形は、 定義１ー２２の補足２ による。
• 辺は、 定義１ー１９の補足 による。
• 比の積は、 定義６ー５ による。
• 比は、 定義５ー３ による。

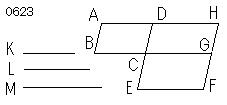
ＡＣ、ＣＦを
　角ＢＣＤが角ＥＣＧに等しい
　等角な２つの平行四辺形とせよ。

• 命題６ー１４の補足４（作図.１組の角が等しい（よって等角な）平行四辺形）
  による。
• 　平行四辺形ＡＣ[ＣＢ,ＣＤ]、線分ＣＧ
  に対して、
  　平行四辺形ＣＦ[ＣＧ,ＣＥ
  　　;;∠ＧＣＥ＝ＢＣＤ,Ｅ;同向側(ＧＣ,ＢＣ,Ｄ)]
  をとっている。
  

平行四辺形ＡＣは
　平行四辺形ＣＦに対し、
　辺の比の積の比をもつと主張する。
　
ＢＣが
　ＣＧと１直線をなすように
　おかれたとせよ。 【・・・(a)】

• 命題６−１４の補足（作図.直線図形の頂点共有と辺の１直線）
  による。
• 　Ｇ'(延長ＢＣ;;ＣＧ'＝ＣＧ)、
  　Ｅ'(同向側(Ｇ'Ｃ,ＢＣ,Ｄ)
  　　;;∠Ｇ'ＣＥ'＝∠ＢＣＤ,ＣＥ'＝ＣＥ)、
  　平行四辺形(ＣＧ',ＣＥ')
  　Ｇ'＞＞Ｇ、
  　Ｅ'＞＞Ｅ、
  をとっている。

そうすれば
　ＤＣもＣＥと１直線をなす。

• (a)、 命題１ー１３（直線と２直角１）
  により、
  　角ＢＣＤとＧＣＤの和は２直角であり、
  　命題の設定により
  　角ＢＣＤはＥＣＧに等しいので、
  公理１ー２（等しいものに等しいものを加える）
  により、
  　角ＥＣＧとＧＣＤの和は２直角である。
  命題１ー１４（直線と２直角２）
  により、
  　ＤＣはＣＥと１直線をなす。
• 　Ｅ;上.延長ＤＣ
  となっている。

平行四辺形ＤＧが完結されたとし、

• 「［平行四辺形の］完結」は、コメント２（命題６ー１４）参照のこと。
• 　平行四辺形ＤＧ(ＣＤ,ＣＧ)
  をとっている。

　線分Ｋが定められ、

• Ｋの位置、大きさは
  　任意である。
  公準１ー１の補足（作図.任意の点をとる）
  により、
  　２点をとり、
  　公準１ー１（作図.直線）
  により
  　線分をひく。
• 　線分Ｋ[]
  をとっている。

　 ＢＣがＣＧに対するように、
　ＫがＬに対し、
　ＤＣがＣＥに対するように、
　ＬがＭに対するとせよ。
　　　　　　【・・・(b)】

• 命題６ー１２（作図.比例第４項）
  による。
• 　線分Ｌ[;;ＢＣ：ＣＧ＝Ｋ：Ｌ]、
  　線分Ｍ[;;ＤＣ：ＣＥ＝Ｌ：Ｍ]
  をとっている。

そうすれば
　ＫがＬに対する比と
　ＬがＭに対する比とは
　辺の比、
　すなわち
　ＢＣがＣＧに対する比と
　ＤＣがＣＥに対する比とに
　同じである。

• 　Ｋ：Ｌ＝ＢＣ：ＣＧ
  　Ｌ：Ｍ＝ＤＣ：ＣＥ
  となっている。

ところが
　 ＫがＭに対する比は
　ＫがＬに対する比と
　ＬがＭに対する比との積である。 　　　　　　【・・・(c)】

• 定義６ー５（合成・積）
  による。
• 　Ｋ：Ｍ＝（Ｌ：Ｍ）×（Ｋ：Ｌ）
  となっている。

それゆえ
　ＫはＭに対し
　辺の比の積の比をもつ。

• 　（ｂ）、 （ｃ）
  　公理の補足３（定義５ー５）(約量(倍量)での代入の原理）
  による。
  
• 　Ｋ：Ｍ＝（ＤＣ：ＣＥ）×（ＢＣ：ＣＧ）
  となっている。

そして
　ＢＣがＣＧに対するように、
　平行四辺形ＡＣがＣＨに対し、

• 命題６ー１（同高の三角形、平行四辺形は底辺と比例）
  による。
• 　ＢＣ：ＣＧ＝平四ＡＣ：平四ＣＨ
  となっている。

　他方
　ＢＣがＣＧに対するように、
　ＫがＬに対するから、

• 　ＢＣ：ＣＧ＝Ｋ：Ｌ
  となっている。

　ＫがＬに対するように、
　ＡＣがＣＨに対する。

• (b), 命題５ー１１（同一の比に同じ比）
  による。
• 　Ｋ：Ｌ＝平四ＡＣ：平四ＣＨ
  となっている。

また
　ＤＣがＣＥに対するように、
　平行四辺形ＣＨがＣＦに対し、

• 命題６ー１（同高の三角形、平行四辺形は底辺と比例）
  による。
• 　ＤＣ：ＣＥ＝平四ＣＨ：平四ＣＦ
  となっている。

　他方
　ＤＣがＣＥに対するように、
　ＬがＭに対するから、

• 　ＤＣ：ＣＥ＝Ｌ：Ｍ
  となっている。

　ＬがＭに対するように、
　平行四辺形ＣＨが平行四辺形ＣＦに対する。

• (b), 命題５ー１１（同一の比に同じ比）
  による。
• 　Ｌ：Ｍ＝平四ＣＨ：平四ＣＦ
  となっている。

そこで
　ＫがＬに対するように、
　平行四辺形ＡＣが平行四辺形ＣＨに対し、
　ＬがＭに対するように、
　平行四辺形ＣＨが平行四辺形ＣＦに対する
　ことが証明されたから、
　等間隔比により
　ＫがＭに対するように、
　ＡＣが平行四辺形ＣＦに対する。

• 命題５ー２２ （等間隔比と同じ比） による。
• 　Ｋ：Ｍ＝平四ＡＣ：平四ＣＦ
  となっている。

ところが
　Ｋは
　Ｍに対し、
　辺の比の積の比をもつ。

• (c) による。
• 　Ｋ：Ｍ＝（ＤＣ：ＣＥ）×（ＢＣ：ＣＧ）
  となっている。

それゆえ
　ＡＣは
　ＣＦに対し辺の比をもつ。

• 命題５ー１１（同一の比に同じ比）
  による。
• 　平四ＡＣ：平四ＣＦ＝（ＤＣ：ＣＥ）×（ＢＣ：ＣＧ）
  となっている。

よって
　等角な２つの平行四辺形は
　互いに
　辺の比の積の比をもつ。
これが証明すべきことであった。

• 　平行四辺形ＢＥを完結させて
  推論すると
  　ＡＣ：ＣＦ＝（ＢＣ：ＣＧ）×（ＤＣ：ＣＥ）
  となる。
  したがって、
  　比の積において、
  　積の順が逆になっても
  　比は同じである。
  (以下、命題６ー２３の補足（比の積は逆順でも同じ）という。)
  　これは、
  　命題５ー２３（乱比例の等間隔比は同じ比）
  によっても
  　論証できる。
  
• 　公準１ー１の補足（作図.点）
  により
  　Ｅ'(ＣＥ)
  をとり、
  　命題１ー３１（作図・平行線）、
  　命題１ー３０の補足(交線に平行な線)
  により
  　交点Ｆ'(ＧＦ,平行線(Ｅ',ＣＧ))
  をとると、
  　定義の補足（命題１ー３４）(平行四辺形・対角線)
  により
  　四角形ＣＦ';平行四辺形、
  　平四ＡＣ(等角)平四ＣＦ'
  である。
  その上、
  　公理１ー８の補足（小さい）
  により
  　平四ＣＦ’＜平四ＣＦ、
  　ＣＥ’＜ＣＥ。
  したがって、
  　命題５ー８（量の大小と比の大小）
  により
  　平四ＡＣ：平四ＣＦ'＜平四ＡＣ：平四ＣＦ、
  　ＤＣ：ＣＥ'＜ＤＣ：ＣＥ。
  よって、
  　（ＤＣ：ＣＥ'）×（ＢＣ：ＣＧ）
  　　＜（ＤＣ：ＣＥ）×（ＢＣ：ＣＧ）。
  ここから、
  　次のことがわかる。
  　小さい比との積は
  　大きい比との積より小さい。
  (以下、命題６ー２３の補足２（小さい比との積は小さい）という。)
  
• 命題６ー２３は、
  　∠ＢＣＤ＝∠ＥＣＧ
  ならば、
  　平四(ＢＣ,ＣＤ)：平四(ＥＣ,ＣＧ)
  　　＝（ＤＣ：ＣＥ）×（ＢＣ：ＣＧ）
  のことである。
  
• 命題６ー２３の補足（比の積は逆順でも同じ）

  前提	作図	推論
  定義
  公準
  公理
  命題		5-23,6-23
  その他

• 命題６ー２３の補足２（小さい比との積は小さい）

  前提	作図	推論
  定義		補(題1-34)
  公準	1-1補
  公理		1-8補
  命題	1-31	1-30補,5-8
  その他

• 命題６ー２３は推論用命題である。

  前提	作図	推論
  定義		6-5
  公準	1-1,1-1補
  公理		1-2,補3(義5-5)
  命題	6-12,6-14補,6-14補4	1-13,1-14,5-11,5-22,6-1
  その他		コ2(題6-14)

前 　　 次 　　 目次 　　頁頭