ユークリッド原論をどう読むか（１０）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第６巻

命題６ー１２（作図.比例第４項）
与えられた３線分に対し、
　第４の比例項を見いだすこと。

• 線分は、 定義の補足（命題１ー１） による。
• 比例は、 定義５ー６ による。
• 項は、 定義５ー８の補足 による。

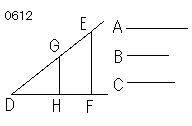
与えられた３線分を
　Ａ、Ｂ、Ｃとせよ。

• 　線分Ａ、Ｂ、Ｃ
  をとっている。

このとき
　Ａ、Ｂ、Ｃに対し、
　第４の比例項を見いださねばならぬ。
　
任意の角ＥＤＦをはさむ
　２線分ＤＥ、ＤＦが
　定められたとせよ。

• 公準１ー１の補足 （作図.任意の点をとる）
  により、
  　３点Ｄ、Ｅ、Ｆをとり、
  　公準１ー１ （作図.直線）
  により、
  　ＤとＥ、ＤとＦを結ぶ。
• 　線分ＥＤ、ＤＦ
  をとっている。

そして
　 ＤＧがＡに、
　ＧＥがＢに、
　また
　ＤＨがＣに等しくされたとせよ。 【・・・(a)】

• 命題１ー３の補足 （作図.等しい線分となる点）
  により、
  　点Ｇ、Ｅ’を、
  　半直線ＤＥ上に
  　ＤＧがＡと、
  　ＧＥ’がＢと等しくなるようにとり、
  　点Ｈを、
  　半直線ＤＦ上に
  　ＤＨがＣと等しくなるようにとる。
  Ｅ’を改めてＥとし、
  　遡って用いている。
• 　Ｇ(ＤＥ;;ＤＧ＝Ａ)、
  　Ｅ'(延長ＤＧ;;ＧＥ'＝Ｂ)、
  　Ｈ(ＤＦ;;ＤＨ＝Ｃ)
  をとっている。
  　Ｅ'をＥ
  としている。

そして
　ＧＨが結ばれ、

• 公準１ー１ （作図.直線）
  による。
• 　線分ＧＨ
  をとっている。

　 Ｅを通りＧＨに平行に
　ＥＦがひかれたとせよ。 【・・・(b)】

• 命題１ー３１ （作図・平行線）
  により、
  　ＥＦ’をひく。
  命題１ー３０の補足 (交線に平行な線)
  により、
  　ＥＦ’はＤＦと交わり、
  　その交点を改めてＦとし、
  　遡って用いている。
• 　Ｆ'(ＤＦ;;ＧＨ‖ＥＦ')
  をとっている。
  　Ｆ'をＦ
  としている。

そうすれば
　ＧＨは
　三角形ＤＥＦの１辺ＥＦに平行《にひかれた》［である］から、

• (b) による。

　 ＤＧがＧＥに対するように、
　ＤＨがＨＦに対する。 【・・・(c)】

• 命題６ー２ （三角形の辺の平行線による辺の比例区分）
  による。
• 　ＤＧ：ＧＥ＝ＤＨ：ＨＦ
  となっている。

ところが
　ＤＧはＡに、
　ＧＥはＢに、
　ＤＨはＣに等しい。

• (a) による。
• 　ＤＧ＝Ａ、
  　ＧＥ＝Ｂ、
  　ＤＨ＝Ｃ
  となっている。

したがって
　ＡがＢに対するように、
　ＣがＨＦに対する。

• (c), 命題５ー１１の補足２ （等しい量は同じ比をもつ） 、
  命題５ー１１ （同一の比に同じ比）
  による。
• 　Ａ：Ｂ＝Ｃ：ＨＦ
  となっている。

よって
　与えられた３線分Ａ、Ｂ、Ｃに対し、
　第４の比例項ＨＦが見いだされた。
これが作図すべきものであった。

• 命題６ー２の補足と同じである。
  命題６ー５（辺が比例する三角形は等角）、
  命題６ー６（２辺が比例し挟角が等しい三角形は等角） 、
  命題６ー７（２辺が比例、挟角以外が等しくて等角となる場合）
  　の証明を
  　仮想的な命題の設定ではなく
  　現実的な命題の設定上で行うために、
  　前以て証明しておいた。
• 命題６ー１２は、
  　線分Ａ、Ｂ、Ｃ
  に対して、
  　線分ＥＤ、ＤＦ、
  　Ｇ(ＤＥ;;ＤＧ＝Ａ)、
  　Ｅ'(延長ＤＧ;;ＧＥ'＝Ｂ)、
  　Ｈ(ＤＦ;;ＤＨ＝Ｃ)、
  　Ｆ'(延長ＤＨ;;ＧＨ‖Ｅ'Ｆ')
  をとれば、
  　Ａ：Ｂ＝Ｃ：ＨＦ'
  のことである。
• 命題６ー１２は作図用命題である。

  前提	作図	推論
  定義
  公準	1-1,1-1補
  公理
  命題	1-3補,1-30補,1-31	5-11,5-11補,6-2
  その他

前 　　 次 　　 目次 　　頁頭