ユークリッド原論をどう読むか（９）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第５巻

命題５ー２２（等間隔比と同じ比）
もし
　任意個の量と
　それらと同じ個数の別の量とがあり、
　２つずつとられたとき
　同じ比をなすならば、
　等間隔比により
　それらは同じ比をなすであろう。

• 量は、 定義５ー１の補足 による。
• 個数は、定義５ー１７の補足 による。
• 同じ比は、定義５ー５ による。
• 等間隔比は、定義５ー１７ による。

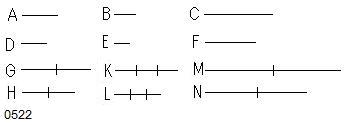
任意個の量Ａ、Ｂ、Ｃと
　それらと同じ個数の別の量Ｄ、Ｅ、Ｆとがあり、
　２つずつとられたとき
　同じ比をなす、
　すなわち
　ＡがＢに対するように、ＤがＥに対し、
　ＢがＣに対するように、ＥがＦに対するとせよ。

• 同じ比をもつ線分の作図（仮想的）は、
  　コメント２（命題５ー４）参照のこと。
• 　量Ａ、Ｂ、Ｃ、Ｄ
  に対して、
  　Ｅ[;;Ａ：Ｂ＝Ｄ：Ｅ]、
  　Ｆ[;;Ｂ：Ｃ＝Ｅ：Ｆ]
  をとっている。

等間隔比により
　それらが同じ比をなすであろう
　と主張する。

• 任意個の命題を
  　３個の場合で推論しようとしている。
  　準一般的な証明である。
  　コメント２（命題５ー１）参照のこと。

Ａ、Ｄの［任意の］同数倍Ｇ、Ｈと
　Ｂ、Ｅの別の任意の同数倍Ｋ、Ｌと
　さらに
　Ｃ、Ｆの別の任意の同数倍Ｍ、Ｎとが
　とられたとせよ。【・・・(a)】

• 推論の設定である。
• 量の倍は、
  　命題の補足（定義５ー２）（作図.倍量）
  による
• 　(Ｇ、Ｆ)＝ｐ(Ａ、Ｄ)、
  　(Ｋ、Ｌ)＝ｑ(Ｂ、Ｅ)、
  　(Ｍ、Ｎ)＝ｒ(Ｃ、Ｆ)
  をとっている。

そうすれば
　ＡがＢに対するように、ＤがＥに対し、

• 命題の設定 による。
• 　Ａ：Ｂ＝Ｄ：Ｅ
  となっている。

　Ａ、Ｄの同数倍Ｇ、Ｈと
　Ｂ、Ｅの別の［任意の］同数倍Ｋ、Ｌとが
　とられたから、

• (a) による。
• 　(Ｇ、Ｆ)＝ｐ(Ａ、Ｄ)、
  　(Ｋ、Ｌ)＝ｑ(Ｂ、Ｅ)
  となっている。

　ＧがＫに対するように、
　ＨがＬに対する。【・・・(1)】

• 命題５ー４ （同じ比の項の同数倍）
  による。
• 　Ｇ：Ｋ＝Ｈ：Ｌ
  となっている。

同じ理由で
　ＫがＭに対するように、
　ＬがＮに対する。【・・・(2)】

• 命題の設定 ,(a) ,命題５ー４ （同じ比の項の同数倍）
  による。
• 　Ｋ：Ｍ＝Ｌ：Ｎ
  となっている。

そこで
　３つの量Ｇ、Ｋ、Ｍと
　それらと同じ個数の別の量Ｈ、Ｌ、Ｎとがあり、
　２つずつとられたとき
　同じ比をなすから、

• (1) , (2) による。
• 　Ｇ：Ｋ：Ｍ＝Ｈ：Ｌ：Ｎ
  となっている。

　等間隔比により
　もし
　ＧがＭより大きければ、
　ＨもＮより大きく、
　等しければ、等しく、
　小さければ小さい。

• 命題５ー２０ 命題５ー２０（等間隔項の大等小）
  による。
• 　Ｇ(＜、＝、＞)Ｍ
  ならば、
  　Ｈ(＜、＝、＞)Ｎ
  となっている。

そして
　Ｇ、ＨはＡ、Ｄの同数倍であり、
　Ｍ、ＮはＣ、Ｆの別の［任意の］同数倍である。

• (a) による。
• 　(Ｇ、Ｈ)＝ｐ(Ａ、Ｄ)、
  　(Ｍ、Ｎ)＝ｒ(Ｃ、Ｆ)
  となっている。

それゆえ
　ＡがＣに対するようにＤがＦに対する。

• 定義５ー５ （同じ比）
  による。
• 　Ａ：Ｃ＝Ｄ：Ｅ
  となっている。

よってもし
　任意個の量と
　それらと同じ個数の別の量とがあり、
　２つずつとられたとき同じ比をなすならば、
　等間隔比により
　それらは同じ比をなすであろう。
これが証明すべきことであった。

• ３個の場合が証明できれば、
  　２番目をないものとできるから、
  　任意の個数でも
  　１個ずつ減らせるので、
  　論証が完了する。
• 　定義６ー５（合成・積）の定義の根拠
  である。
• 命題５ー２２は、
  　Ａ：Ｂ＝Ｄ：Ｅ、
  　Ｂ：Ｃ＝Ｅ：Ｆ
  ならば、
  　Ａ：Ｃ＝Ｄ：Ｆ
  ということである。
• 命題５ー２２は推論用命題である。

  前提	作図	推論
  定義		5-5
  公準
  公理
  命題		補(義5-2),5-4,5-20
  その他		コ2(題5-1),コ2(題5-4)

前 　　 次 　　 目次 　　頁頭