ユークリッド原論をどう読むか（１４）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第１０巻
　
命題１０ー６（量が数：数なら通約可）
（作図.長さで数：数となる線分）
（作図.平方で数：数となる線分）
（作図.長さ・平方で通約可の線分)
もし
　２つの量が
　互いに数が数に対する比をもつ
ならば、
　それらの量は通約できる
であろう。

• 量は、
  定義５ー１の補足による。
• 数は、
  定義７ー２による。
• 対するは、
  定義の補足３（命題５ー１１）による。
• 比は、
  定義５ー３による。
• 通約は、
  定義１０ー１による。

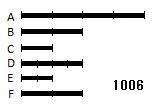
　２つの量Ａ、Ｂが
　互いに
　数Ｄが数Ｅに対する比をもつ
とせよ。

• 　「量（について）・・・とせよ」は、
  　コメント６（命題５ー１）
  　参照のこと。
  
• 「数（について）・・・とせよ」は、
  　コメント４（命題７ー１）
  参照のこと
  

　量Ａ、Ｂは通約できる
と主張する。

　Ａが
　Ｄのなかにある単位の個数と同数の、
　等しい部分に分けられ、
　Ｃが
　それらの１つに等しい
とせよ。
　　　　　　[......(ａ)]

• 　命題６ー９（作図.線分のｎ分の１） による。 　
  
• 　Ｃ＝Ａ／Ｄ
  となっている。

そして
　Ｆが
　Ｅのなかにある単位の個数と同数の、
　Ｃに等しい量から成る
とせよ。
　　　　　　[......(ｂ)]

• 　命題の補足（定義５ー２）（作図.倍量） による。
• 　Ｆ＝Ｅ×Ｃ
  となっている。

そうすれば
　Ｄのなかにある単位の数と同数の、
　Ｃに等しい量が
　Ａのなかにある

• 　（ａ）による。
• 　Ａ＝Ｄ×Ｃ
  となっている。
  

から、
　単位がＤのいかなる部分であろう
と、
　ＣもＡの同じ部分である。
したがって
　ＣがＡに対するように、
　単位がＤに対する。
　　　　　　[......(１)]

• 　前節、
  　定義５ー５（同じ比）
  による。
• 　Ｃ：Ａ＝単位：Ｄ
  となっている。

そして
　単位は数Ｄを割り切る。

• 　定義７ー２（数）
  による。
  
• 　単位｜Ｄ
  となっている。

したがって
　ＣもＡを割り切る。
　　　　　　[......(２)]

• 　定義５ー５（同じ比）
  による。
  
• 　Ｃ｜Ａ
  となっている。

そして
　ＣがＡに対するように、
　単位がＤに対する

• 　（１）による。
• 　Ｃ：Ａ＝単位：Ｄ
  となっている。

から、
逆に
　ＡがＣに対するように、
　数Ｄが単位に対する。
　　　　　　[......(３)]

• 　前節、
  　命題５ー７の系(比例すれば逆も比例)
  による。
• 　Ａ：Ｃ＝Ｄ：単位
  となっている。

また
　Ｅのなかにある単位の個数と同数の、
　Ｃに等しい量が
　Ｆのうちにある

• 　（ｂ）による。
• 　Ｆ＝Ｅ×Ｃ
  となっている。
  

から、
　ＣがＦに対するように、
　単位がＥに対する。

• 　前節、
  　定義５ー５（同じ比）
  による。
• 　Ｃ：Ｆ＝単位：Ｅ
  となっている。

そして
　ＡがＣに対するように
　Ｄが単位に対する
ことが先に証明された。

• 　（３）による。
• 　Ａ：Ｃ＝Ｄ：単位
  となっている。
  

したがって
　等間隔比により
　ＡがＦに対するように、
　ＤがＥに対する。

• 　前節、前々節、
  　命題５ー２２（等間隔比と同じ比）
  による。
• 　Ａ：Ｆ＝Ｄ：Ｅ
  となっている。

ところが
　ＤがＥに対するように、
　ＡがＢに対する。

• 　命題の設定による。
• 　Ｄ：Ｅ＝Ａ：Ｂ
  となっている。
  

したがって
　Ａは
　Ｂに対するように、
　Ｆにも対する。

• 　前節、前々節、
  　命題５ー１１（同一の比に同じ比）
  による。
• 　Ａ：Ｂ＝Ａ：Ｆ
  となっている。

それゆえ
　ＡはＢ、Ｆの双方に対し
　同じ比をもつ。

したがって
　ＢはＦに等しい。

• 　前節、
  　命題５ー９（同一比の量）
  による。
• 　Ｂ＝Ｆ
  となっている。

そして
　ＣはＦを割り切る。

• 　（ｂ）による。
• 　Ｃ｜Ｆ
  となっている。

ゆえに
　Ｂをも割り切る。

• 　前節、前々節、
  　公理の補足３（定義５ー５）(約量(倍量)での代入の原理）
  による。
• 　Ｃ｜Ｂ
  となっている。

ところが
また
　Ａをも割り切る。

• 　（２）による。
• 　Ｃ｜Ａ
  となっている。

それゆえ
　ＣはＡ、Ｂを割り切る。

• 　前節、前々節による。
• 　Ｃ｜（Ａ、Ｂ）
  となっている。

したがって
　ＡはＢと通約できる。

• 　前節、
  　定義１０ー１（通約）
  による。
• 　Ａ∩Ｂ
  となっている。
  

よって
　２つの量が互いに云々

• 　云々は、
  　「数が数に対する比をもつ
  　ならば、
  　　それらの量は通約できる
  　であろう。」
  である。

　系
これから
　次のことが明らかである。

すなわち
もし
　２つの数、たとえばＤ、Ｅと、
　１つの線分、たとえばＡがある
とすれば、
　数Ｄが数Ｅに対するように、
　与えられた線分［Ａ］が他の線分［Ｆ］に対する
ようにすることができる。
(以下、命題１０ー６の系 （作図.線分で数：数となる線分）という。)

• 　命題７ー１１の補足(構成.比例する数の作図)
  による。
  　量Ａと、数Ｄ、Ｅ
  により、
  　量Ｆを作図した
  （ａ）、 （ｂ）
  を参照のこと
• 　Ａ：Ｆ＝Ｄ：Ｅ（数）
  となっている。

そして
もし
　Ａ、Ｆの比例中項、たとえばＢがとられた
とすれば、

• 　Ｂの作図は、
  　命題６ー１３（作図.２線分の比例中項）
  による。
• 　Ａ：Ｂ＝Ｂ：Ｆ
  となっている。

　ＡがＦに対するように、
　Ａ上の正方形がＢ上の正方形に対する
であろう、

• 　前節、
  　命題６ー２０（相似多角形の相似三角形分解と２乗の比）
  による。
• 　sq(_Ａ)：sq(_Ｂ)
  　＝（Ａ：Ｂ）^2
  　＝Ａ：Ｆ
  となっている。
  

すなわち
　第１の線分が第３の線分に対するように、
　第１の線分上の図形が
　第２の線分上の相似でかつ相似な位置に
　描かれた図形に対する
であろう。

ところが
　ＡがＦに対するように、
　数Ｄが数Ｅに対する。

• 　命題１０ー６の系（作図.長さで数：数となる線分）
  による。
  
• 　Ａ：Ｆ＝Ｄ：Ｅ
  となっている。

したがって
　数Ｄが数Ｅに対するように、
　線分Ａ上の図形が
　線分Ｂ上の図形に対する
　(以下、命題１０ー６の系２（作図.平方で数：数となる線分）という。)
ことになっている。

• 　前節、前々節、
  　命題５ー１１（同一の比に同じ比）
  による。
• 　sq(_Ａ)：sq(_Ｂ)＝Ｄ：Ｅ（数）
  となっている。

　これが証明すべきことであった。

• 　命題１０ー６の系（作図.長さで数：数となる線分）
  　あるいは、
  　命題１０ー６の系２（作図.平方で数：数となる線分）
  により
  　作図した
  ならば、
  　命題１０ー６（量が数：数なら通約可）
  により、
  　長さにおいて、
  　あるいは、
  　平方において通約な線分を
  　ひくことができる。
  　(以下、命題１０ー６の系３（作図.長さ・平方で通約可の線分)という。)
  　本命題の系３
  により、
  　通約できる線分を
  　実際に作図できるようになった。
  　コメント３（命題１０ー３）
  　を参照のこと。
  
• 命題１０ー６は、
  　Ａ：Ｂ＝ｍ：ｎ（数）
  ならば、
  　Ａ∩Ｂ
  のことである。
  
• 命題１０ー６の系 （作図.線分で数：数となる線分）

  前提	作図	推論
  定義
  公準
  公理
  命題	7-11補,10-6
  その他

• 前提	作図	推論
  定義
  公準
  公理
  命題		6-20,10-6系
  その他

• 命題１０ー６の系３（作図.長さ・平方で通約可の線分)

  前提	作図	推論
  定義
  公準
  公理
  命題	10-6系,10-6系2	10-6
  その他

• 命題１０ー６は推論用命題である。
  

  前提	作図・作図	推論
  定義		5-5,7-2
  公準
  公理		補3(義5-5)
  命題	補(義5-2),6-13	5-7系,5-9,5-11,5-22,6-20
  その他	コ6(題5-1), コ4(題7-1)

前 　　 次 　　 目次 　　頁頭