ユークリッド原論をどう読むか（１１）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第７巻
　
命題７ー１１（残りも全体と比例）
（作図.比例する数）
もし
　全体が全体に対する
ように、
　引き去られた数が
　引き去られた数に対する
ならば、
　残りも残りに対し、
　全体が全体に対する
ようであろう。

• 対する・ようには 定義の補足３（命題５ー１１） による。
• 数は、 定義７ー２による

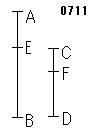
　ＡＢ全体がＣＤ全体に対する
ように、
　引き去られたＡＥが
　引き去られたＣＦに対する
とせよ。

• 「数（について）・・・とせよ」は、
  コメント４（命題７ー１） 参照のこと。
  図は、ＡＢ＝９、ＣＤ＝６、ＡＥ＝３、ＣＦ＝２による。
  
• 
  　比例する数（同じ倍数、商が等しい数）の作図は、
  　定義７ー２１（比例）
  にしたがうと、
  　命題７ー６の補足２(構成.同じ等分和となる第３、４数)
  により
  　作図することができる。
  （以下、命題７ー１１の補足 (構成.比例する数の作図)という。）
  
• 　数ＣＤと
  　等分和ＡＢ[ＣＤ]
  に対して、
  　点Ｅ[ＡＢ]、点Ｆ(ＣＤ)
  　　;ＡＢ：ＣＤ＝ＡＥ：ＣＤ
  をとっている。

　残りのＥＢも残りのＦＤに対し、
　ＡＢ全体がＣＤ全体に対する
ようである
と主張する。

　ＡＢがＣＤに対するように、
　ＡＥがＣＦに対する

• 　命題の設定による。
• 　ＡＢ：ＣＤ＝ＡＥ：ＣＦ
  となっている。

から、
　ＡＢがＣＤのいかなる《約数》[等分]
　または
　《約数》[等分]和であろうと、
　ＡＥもＣＦの同じ《約数》[等分]
　または
　《約数》[等分]和である。

• 　定義７ー２１（比例）
  による。
• 　等分和(ＡＢ,ＣＤ)＝等分和(ＡＥ,ＣＦ)＝ｎ／ｍ
  となっている。

したがって
　残りのＥＢも
　残りのＦＤの、
　ＡＢがＣＤの《約数》[等分]
　または
　《約数》[等分]和であるのと
　同じ《約数》[等分]
　または
　《約数》[等分]和である。

• 命題７ー７（差も同じ等分）、
  命題７ー８（差も同じ等分和）
  による。
• 　等分和(ＥＢ,ＦＤ)＝等分和(ＡＢ,ＣＤ)＝(ｍ−ｎ)／ｍ
  となっている。

よって、
　ＥＢがＦＤに対するように、
　ＡＢがＣＤに対する。

• 　定義の補足（命題７ー６） (同じ等分和)
  による。
• ＥＢ：ＦＤ＝ＡＢ：ＣＤ
  となっている。

これが証明すべきことであった。

• 命題７ー１１は、
  　数ＣＤと
  　等分和ＡＢ[ＣＤ]
  に対して、
  　点Ｅ[ＡＢ]、点Ｆ(ＣＤ)
  　　;ＡＢ：ＣＤ＝ＡＥ：ＣＦ＝ｑ：ｐ
  をとれば、
  　ＥＢ：ＦＤ＝ＡＢ：ＣＤ＝ｑ：ｐ
  すなわち、
  　ＡＢーＡＥ：ＣＤーＣＦ
  　＝ＡＢ：ＣＤ＝ｑ：ｐ
  のことである。
• 命題７ー１１の補足（作図.比例する数）は作図用命題である。

  前提	作図	推論
  定義		7-21
  公準
  公理
  命題	7-6補2
  その他

  　
  
• 命題７ー１１は推論用命題である。
  

  前提	作図	推論
  定義		補3(題5-11),7-2,7-21
  公準
  公理
  命題	7-11補	7-7,7-8
  その他	コ4(題7-1)

前 　　 次 　　 目次 　　頁頭