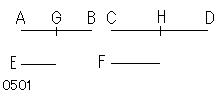ユークリッド原論をどう読むか（９501）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第５巻

命題５ー１（同数倍の和１）
同じ倍数　 準一般的な証明 （１対１対応） （複合１対１対応） 準一般の一般化 任意の量

もし
　任意個の量があり、
　それと同数の他の《任意個の》量の
　　それぞれ同数倍であるならば、
　それらの量の１つが１つの何倍であろうと、
　全体も
　全体の同じ倍数であろう。

• 量は、 定義５ー１の補足 による。
• ２つめの「任意個の」は、
  　１つめの「任意個」のことであり、
  　「それと同数の」と直前で限定してあるので、
  　記述されない方がよい。
• 同数倍は、 定義５ー５の補足 による。
• 同じ倍数とは、
  　 定義の補足（公理１ー５） にいう
  　　ｎ倍における個数分のｎが
  　等しいということである。
  したがって、
  　同じ倍数であれば、
  　倍量が倍される量に対して
  　同じ比をもつ。
  （以下、定義の補足（命題５ー１）(同じ倍数)という。）
  定義５ー５の補足にいう
  「同数倍」は
  　同じ個数分という量に注目し、
  「同じ倍数」は
  　個数分の個数に注目している。

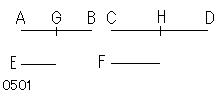
任意個の量ＡＢ、ＣＤが
　それと同数の他の《任意個の》量Ｅ、Ｆの
　　それぞれ同数倍であるとせよ。

• 　量Ｅ、Ｆ
  に対して
  　量ＡＢ＝ｎ×Ｅ、
  　量Ｆ(;;倍数(ＡＢ,Ｅ)＝倍数(ＣＤ,Ｆ))
  をとっている。

ＡＢが
　Ｅの何倍であろうと、
　ＡＢ、ＣＤの和も
　Ｅ、Ｆの和の同じ倍数であろう
　と主張する。

• 任意の量を表す線分は
  　公準１ー１（作図.直線）により
  　作図可能であるが、
  　命題にいう量は
  　その条件の当てはまる量を描き、
  　考察について
  　可能な範囲で一般的に行う
  　ということになる。
  (以下、コメント６（命題５ー１） (任意の量)という。)
  
• 量の倍は、 命題の補足（定義５ー２）（作図.倍量）、
  量の和は、 命題の補足（定義５ー１４）（作図.量の和）
  による。

ＡＢはＥの、
　ＣＤはＦの同数倍であるから、

• 命題の設定 による。
• 　倍数(ＡＢ,Ｅ)＝倍数(ＣＤ,Ｆ)
  となっている。

　ＡＢの中にある
　　Ｅに等しい量と同じ個数の、
　Ｆに等しい量が
　ＣＤのなかにある。【・・・(1)】

• 定義５ー５の補足（同数倍）
  による。
• 　個数(ＡＢ,Ｅ)＝個数(ＣＤ,Ｆ)＝ｎ
  となっている。

ＡＢが
　Ｅに等しい量ＡＧ['＝G1G'1、･･･、GiG'i、･･･、GnG'n＝]ＧＢに、
　ＣＤが
　Ｆに等しい量ＣＨ['＝H1H'1、･･･、HiH'i、･･･、HnH'n＝]ＨＤに
　分けられたとせよ。【・・・(a)】

• 推論の設定である。
• 準一般的な証明の一般化の方法である。
  今後、
  本文中では、
  　ＡＧ、［ＧiＧ'i、］ＧＢで、
  コメント内では、
  　ＧiＧ'iで、
  準一般的な証明の一般化、
  　ＡＧ'＝Ｇ1Ｇ'1、・・・、ＧiＧ'i、・・・、ＧnＧ'n＝ＧＢ、
  　(ただし、Ｇ'i＝Ｇi+1)
  を簡潔に表記する。
  以下、コメント５（命題５ー１）(準一般の一般化)という。
  　ΣＧiＧ'i
  　＝ＡＧ'＋Ｇ2Ｇ'2＋・・・
  　　＋ＧiＧ'i＋・・・
  　　＋Ｇn-1Ｇ'n-1＋ＧＢ
  である。
• 　ＧiＧ'i＝Ｅ、
  　ＨiＨ'i＝Ｆ
  となっている。

そうすれば
　ＡＧ、[ＧiＧ'i、]ＧＢの個数［ｎ］は、
　ＣＨ、[ＨiＨ'i、]ＨＤの個数［ｎ］に
等しいであろう。【・・・(2)】

• (1) による。
• 　個数(ＧiＧ'i)＝個数(ＨiＨ'i)＝ｎ
  となっている。

そして
　ＡＧはＥに、
　ＣＨはＦに
　　等しいから、

• (a) による。
• 　ＡＧ＝Ｅ、
  　ＣＨ＝Ｆ
  となっている。

　ＡＧはＥに、
　ＡＧ、ＣＨの和はＥ、Ｆの和に
　等しい。

• 公理１ー２（等しいものに等しいものを加える）
  による。
• 　ＡＧ＝Ｅ、
  　ＡＧ＋ＣＨ＝Ｅ＋Ｆ
  となっている。

同じ理由で
　[GiG'iはＥに、
　GiG'i、HiH'iの和はＥ、Ｆの和に、]
　ＧＢはＥに、
　ＧＢ、ＨＤの和はＥ、Ｆの和に
　等しい。

• 　ＧiＧ'i＝Ｅ、
  　ＧiＧ'i＋ＨiＨ'i＝Ｅ＋Ｆ、
  　ＧＢ＝Ｅ、
  　ＧＢ＋ＨＤ＝Ｅ＋Ｆ
  となっている。　

それゆえ
　ＡＢのなかにある
　　Ｅに等しい量と同数［ｎ］の、
　Ｅ、Ｆ［の和］に等しい量が
　ＡＢ、ＣＤ［の和］のなかにある。

• (2)、公理の補足３（命題５ー１）(１対１対応)
  による。
• 　個数(ＡＢ,Ｅ)＝個数(ＡＢ＋ＣＤ,Ｅ＋Ｆ)＝ｎ
  となっている。

ゆえに
　ＡＢが
　Ｅの何倍であろうと
　ＡＢ、ＣＤの和も
　Ｅ、Ｆの和の同じ倍数である。

• 定義の補足（命題５ー１） (同じ倍数)
  による。
• 　倍数(ＡＢ,Ｅ)＝倍数(ＡＢ＋ＣＤ,Ｅ＋Ｆ)＝ｎ
  となっている。

よってもし
　任意個の量があり、
　それと同数の他の［任意個の］量の
　　それぞれ同数倍であるならば、
　それらの量の１つが
　　１つの何倍であろうと、
　全体も
　　全体の同じ倍数であろう。
これが証明すべきことであった。

• 任意の個数に関する
  　原論の証明は、
  　準一般的な証明といわれ、
  　典型例である場合の、
  　ＡＢがＥの２個分の場合をもって
  　図を描いて論じている。
  そこでの論証の進め方は
  　可能な限り
  　一般的に通じるよう、
  　工夫されている。
  （以下、コメント２（命題５ー１）(準一般的な証明)という。）
  若干補足して、
  　一般的に通じるようにした。
  
• ２つの量が、
  　それぞれ、
  　重ならない部分に分けられ、
  　一方の部分と他方の部分とが
  　　過不足なく対応させられる
  　ならば、
  　またその時だけ、
  　２つの量は同数の部分からなる。
  （以下、公理の補足３（命題５ー１）(１対１対応)という。）
  今日的にいえば、
  　１対１対応により、
  　個数を確定することである。
  原論においては、
  　公理以上に当然のものとして
  　扱われている。
• ２つの量が、
  　それぞれ
  　同数の重らない部分に分けられ、
  　一方の部分と対応する他方の部分が、
  　それぞれ
  　同数の互いに重ならない小部分に
  　　分けられるならば、
  　２つの量は
  　同数の小部分からなる。
  （以下、命題５ー１の補足４（複合１対１対応）という。）
  一方の量の
  　それぞれの部分をなす小部分と、
  　その部分に対応する
  　　他方の量の部分をなす小部分とは、
  　同数であるから、
  　公理の補足３（命題５ー１）(１対１対応)
  により
  　過不足なく対応する。
  他の対応する部分においても
  　同様であるから、
  　一方の量の全体をなす小部分は
  　他方の量の全体をなす小部分と
  　過不足なく対応する。
  公理の補足３（命題５ー１）(１対１対応)
  により、
  　２つの量は同数の小部分からなることがわかる。
• 命題５ー１は、
  　倍数(ＡＢ,Ｅ)＝倍数(ＣＤ,Ｆ)＝ｎ
  ならば、
  　倍数(ＡＢ,Ｅ)＝倍数(ＡＢ＋ＣＤ,Ｅ＋Ｆ)＝ｎ
  すなわち、
  　ｎＥ＋ｎＦ＝ｎ(Ｅ＋Ｆ)
  のことである。
  なお、
  　ｎは個数である。
• 命題５ー１の補足４（複合１対１対応）

  前提	作図	推論
  定義
  公準
  公理		補3(題5-1)
  命題
  その他

• 命題５ー１は推論用命題である。

  前提	作図	推論
  定義		5-5補,補(題5-1)
  公準
  公理		1-2,補3(題5-1)
  命題	補(義5-2),補(義5-14)
  その他		コ2(題5-1)

前 　　 次 　　 目次 　　頁頭