0917 ユークリッド原論９

ユークリッド原論をどう読むか（１３）
頁末　　前　　次　　目次

ユークリッド原論

第９巻
　
命題９ー１７（順次比例で外項が互に素と末項）
もし
　順次に比例する任意個の数があり、
　その外項が互いに素である
ならば、
　第１の数が第２の数に対するように、
　末項が他のいかなる数にも対さない
であろう。

順次に比例は、
定義の補足（命題８ー１）による。
数は、
定義７ー２による。
外項は、
定義の補足（命題６ー１６）による。
互いに素は、
定義７ー１３による。
対する・ようには、
定義の補足３（命題５ー１１）による。
末項は、
定義の補足（命題８ー７）による。

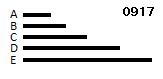
　順次に比例する任意個の
　数Ａ、Ｂ、Ｃ、Ｄがある
とし、
　それらの外項Ａ、Ｄが
　互いに素である
とせよ。

　「数（について）・・・とせよ」は、
　コメント４（命題７ー１）
　参照のこと。
　準一般的な証明である。
　コメント２（命題５ー１）
　参照のこと。
　Ａ、Ｂ、Ｃ、Ｄは順次に比例
　Ａ⊥Ｄ
となっている。

　ＡがＢに対するように、
　Ｄは他のいかなる数にも対さない
と主張する。

もし可能ならば、

　「もし可能ならば」は、
　コメント２(命題１－７）
　参照のこと。

　ＡがＢに対するように、
　ＤがＥに対するとせよ。

　背理法の仮定である。。
　Ａ：Ｂ＝Ｄ：Ｅ
としている。

そうすれば
　いれかえて
　ＡがＤに対するように、
　ＢがＥに対する。

　前節、
　命題７ー１３（比例４数はいれかえても比例）
による。
　Ａ：Ｄ＝Ｂ：Ｅとなっている。

ところが
　Ａ、Ｄは［互いに］素であり、

　命題の設定による。
　Ａ⊥Ｄ
となっている。

　［互いに］素であるものは最小であり、

　前節、
　命題７ー２１（互いに素な数は同じ比の最小）
による。
　Ａ：Ｄ（最小）＝Ｂ：Ｅ
となっている。

　最小である数は
　同じ比をもつ数を割り切り、
　前項が前項を、
　後項が後項を割り切り、
　その商は等しい。

　前節、
　命題７ー２０（同じ比なら最小のが割り切る）
による。

ゆえに
　ＡはＢを割り切る。
となっている。
　　　　　　[......(１)]

　Ａ｜Ｂ、Ｄ｜Ｅ

そして
　ＡがＢに対するように、
　ＢがＣに対する。

　命題の設定による。
　Ａ：Ｂ＝Ｂ：Ｃ
となっている。

ゆえに
　ＢもＣを割り切る。
　　　　　　[......(２)]

　前節、
　定義７－２１（比例）
による。
　Ｂ｜Ｃ
となっている。

したがって
　ＡもＣを割り切る。
　　　　　　[......(３)]

　前節、 （１）
　公理の補足２（命題７ー４）（約数(倍数)での代入の原理）
による。
　Ａ｜Ｂ、Ｂ｜Ｃ
により、
　Ａ｜Ｃ
となっている。

そして
　ＢがＣに対するように、
　ＣがＤに対し、

　命題の設定による。
　Ｂ：Ｃ＝Ｃ：Ｄ
となっている。

　ＢがＣを割り切る

　（２）による。

から、
　ＣもＤを割り切る。

　前節、前々節
　公理の補足２（命題７ー４）（約数(倍数)での代入の原理）
による。
　Ｃ｜Ｄ
となっている。

ところが
　ＡはＣを割り切った。

　（３）による。
　Ａ｜Ｃ
となっている。

それゆえ
　ＡはＤをも割り切る。

　前節、前々節
　公理の補足２（命題７ー４）（約数(倍数)での代入の原理）
による。
　Ａ｜Ｄ
となっている。

しかも
　自分白身をも割り切る。

　命題７－２の補足２（数は自分自身を割り切る）
による。

ゆえに
　Ａは互いに素である
　Ａ、Ｄを割り切る。

　前節、前々節による。

これは不可能である。

　前節、
　定義７ー１３（互いに素）
による。

したがって
　ＡがＢに対するように、
　Ｄは他のいかなる数にも対さない
であろう。

　背理法による。

　これが証明すべきことであった。

命題９ー１７は、
　Ａ1、Ａ2、Ａ3、…、Ａn；順次比例、
　Ａ1、Ａn；互いに素
ならば、
　任意の数Ｂについて、
　Ａl:Ａ2≠Ａn：Ｂ
のことである。
命題９ー１７は推論用命題である。

前提作図推論
定義 7-13,7-21
公準
公理 補2(題7-4)
命題 7-2補2,7-13,7-20,7-21
その他 コ4(題7-1) コ2(題1-7),コ2(題5-1),背理法

前　　次　　目次　　頁頭

前提	作図	推論
定義		7-13,7-21
公準
公理		補2(題7-4)
命題		7-2補2,7-13,7-20,7-21
その他	コ4(題7-1)	コ2(題1-7),コ2(題5-1),背理法