ユークリッド原論をどう読むか（１１）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第７巻
　
命題７ー４（小さい数は等分数か等分和数）
（約数・等分数(倍数)に等しいもの、等しいものの約数・等分数(倍数)）
（約数・等分数(倍数)での代入の原理）
(大きい数は《約数和》[等分和数](倍数))
すべての小さい数は
　大きい数の《約数》[等分数]か
　または
　《約数和》[等分和]である。

• 小さいは、 公理１ー８の補足 による。
• 数は、 定義７ー２ による。
• 大きいは、 公理１ー８ による。
• 《約数》[等分数]は、 定義７ー３ による。
• 《約数和》[等分和数]は、この命題において定義される。
  　定義７ー４ の根拠となっている。
  

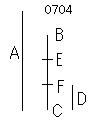
Ａ、ＢＣを２つの数とし、
　ＢＣが小さいとせよ。

• 「数（について）・・・とせよ」は、
  　コメント４（命題７ー１） 参照のこと。
  図は８と６による。
  　命題の補足（定義７ー２）(作図.数ｎ)
  による。
• 　数Ａ
  に対して、
  　数ＢＣ[;;＜Ａ]
  をとっている。

ＢＣは
　Ａの《約数》[等分数]か
　または
　《約数和》[等分和数]である
　と主張する。
　
Ａ、ＢＣは
　互いに素であるか
　あるいは
　ないか
　である。

• 「・・・か、あるいは、・・・かである」は、
  　コメント(命題７ー３）参照のこと。
• 　「互いに素による場合分け」は、
  　コメント４(命題７ー３）
  　参照のこと。

まず
　Ａ、ＢＣが互いに素であるとせよ。

• 　Ａ(互いに素)ＢＣ
  としている。

そうすれば
　ＢＣが
　そのなかにある単位に
　分けられるとき、

• 定義７ー１３（互いに素）
  による。
• 共通に量り切るものは
  　単位しかない。
  数は
  　単位の倍量である。
  
• 　単位｜ＢＣ
  となっている。

　ＢＣのなかにある
　おのおのの単位は
　Ａの《約数》[等分数]であろう。

• 単位によって
  　量り切られる
  　という意味である。
  
• 　「等分数」ではなく「約数」
  としてしまうと、
  　単位を
  　約数に含める
  ことになる。
  
• 　等分(単位.Ｂ,Ａ)
  となっている。

したがって
　ＢＣはＡの《約数和》[等分和数]である。

• 定義７ー４の補足（等分和数）
  の根拠となる。
• 　ＢＣ＝Σ(等分(単位,Ａ).Ａ)
  となっている。これを
  　ＢＣ;等分和数(単位,Ａ)
  とかく。

次に
　Ａ、ＢＣが互いに素でないとせよ。

• 　Ａ¬(互いに素)ＢＣ
  としている。

そうすれば
　ＢＣは
　Ａを割り切るか
　あるいは
　割り切らないか
である。

• 「・・・か、あるいは、・・・かである」は、
  　コメント(命題７ー３）参照のこと。
• 　ＢＣ;(｜Ａ or ¬｜Ａ)
  となっている。

そこでもし
　ＢＣが
　Ａを割り切るならば、

• 場合分け（２-1）である。
• 　ＢＣ｜Ａ
  としている。

　ＢＣはＡの《約数》[等分数]である。

• 定義７ー３(約数・等分数)
  による。
• 　ＢＣ;等分数(ＢＣ,Ａ)
  となっている。

ところがもし
　割り切らないならば、

• 場合分け（２-2）である。
• 　ＢＣ¬｜Ａ
  としている。

　 Ａ、ＢＣの最大公約数Ｄがとられたとし、

• 命題７ー２（構成.最大公約数）
  による。
• 　最大公約数Ｄ(Ａ,ＢＣ)
  をとっている。

　そして
　ＢＣが
　Ｄに等しいＢＥ、《ＥＦ》［ＥiＦi］、ＦＣ
　［、Ｂ＝Ｅ0、Ｅ＝Ｆ0、Ｅi＝Ｆi-1、Ｆ＝Ｆn、Ｃ＝Ｆn+1］に
　分けられたとせよ。 【・・・(a)】

• 　準一般的な証明である。
  　コメント２（命題５ー１）
  　参照のこと。
• 　準一般的な証明の一般化の方法は、
  　コメント５（命題５ー１）
  　参照のこと。
• 　命題７ー２（構成.最大公約数）、
  　定義７ー３(約数・等分数)
  による。
• 　最大公約数Ｄ(Ａ,ＢＣ)
  をとり、
  　ＢＣ＝Σ(ＥiＦi;＝Ｄ)
  としている。

そうすれば
　ＤはＡを割り切るから、
　ＤはＡの《約数》[等分数]である。

• (a)による。
• 　Ｄ;等分数(Ｄ,Ａ)
  となっている。

ところが
　Ｄは
　ＢＥ、Ｅ[i]Ｆ[i]、ＦＣのおのおのに等しい。

• (a)による。
• 　Ｄ;＝ＥiＦi
  となっている。

それゆえ
　ＢＥ、Ｅ[i]Ｆ[i]、ＦＣのおのおのもＡの《約数》[等分数]である。

• 数は単位の倍量であり、
  　量としては
  　定義５ー５の補足（商としての倍数）
  、
  　公理１ー５の補足２（等しいもののｎ倍、ｎ倍に等しいもの）
  により
  　等しいものの同数倍は
  　等しく、
  　公理１ー６の補足３（等しいもののｎ等分、ｎ等分に等しいもの）
  により
  　等しいものの同数等分は
  　等しいので、
  　約数・等分数に等しいものは約数・等分数であり、
  　倍数に等しいものは倍数であり、
  　等しいものの約数・等分数は約数・等分数であり、
  　等しいものの倍数は倍数である。
  （以下、命題７ー４の補足（約数・等分数(倍数)に等しいもの、等しいものの約数・等分数(倍数)）という。）
  　上の補足
  により
  　約数・等分数・倍数に関して
  　代入することができる
  （以下、公理の補足２（命題７ー４）（約数・等分数(倍数)での代入の原理） という。）
• 　等分数(ＥiＦi,Ａ);＝等分数(最大公約数Ｄ(Ａ,ＢＣ),Ａ)
  となっている。

ゆえに
　ＢＣはＡの《約数和》[等分和数]である。

• 定義７ー４の補足（等分和数・倍数）
  の根拠になっている。
• 　ＢＣ;＝Σ(等分(最大公約数Ｄ(Ａ,ＢＣ),Ａ).Ａ)、
  　ＢＣ;等分和数(ＢＣ,Ａ) となっている。

［ したがって、
　第２段階では、
　２つの場合の結果により
　ＢＣはＡの《約数》[等分数]であるか、
　《約数和》[等分和数]である。

したがって、
　第１段階で、
　２つの場合の結果により
　ＢＣはＡの等分数であるか、
　等分和数である。］
　
よって
　すべての小さい数は
　大きい数の《約数》[等分数]か
　または
　《約数和》[等分和数]である。
これが証明すべきことであった。

• 　命題７ー４（小さい数は等分数か等分和数）、
  　定義７ー３(約数・等分数)、
  　定義７ー５（倍数）、
  　定義７ー４の補足 （等分和数・倍数） により、
  　大きい数は
  　小さい数の倍数か等分和数
  すなわち
  　等分和数
  である。
  (以下、命題７ー４の補足３ (大きい数は等分和数(倍数))という。)
  　
• 　分数概念の初出と見ることができる。
  
• 命題７ー４は、
  　数Ａ
  に対して、
  　数ＢＣ[;;＜Ａ]
  をとれば、
  　ＢＣ;(等分数(ＢＣ,Ａ) or 等分和数(ＢＣ,Ａ))
  のことである。
• 命題７ー４の補足（約数・等分数(倍数)に等しいもの、等しいものの約数・等分数(倍数)）

  前提	作図	推論
  定義		5-5補
  公準
  公理		1-5補2,1-6補3
  命題
  その他

• 命題７ー４の補足３ (大きい数は等分和数(倍数))

  前提	作図	推論
  定義		7-3,7-4補,7-5
  公準
  公理
  命題		7-4
  その他

• 命題７ー４は推論用命題である。

  前提	作図	推論
  定義		5-5補,7-3
  公準
  公理		1-5補2
  命題	補(義7-2),7-2
  その他		場合分け,コ(題7-3),コ4(題7-3)

前 　　 次 　　 目次 　　頁頭