ユークリッド原論をどう読むか（１０）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第６巻

命題６ー１６（比例４線分と外項矩形、内項矩形）
外項　内項　
(作図.線分上に矩形と等しい矩形)
もし
　４線分が比例するならば、
　外項にかこまれた矩形は
　内項にかこまれた矩形に等しい。
そしてもし
　外項にかこまれた矩形が
　内項にかこまれた矩形に等しいならば、
　４線分は比例するであろう。

• 線分は、 定義の補足（命題１ー１） による。
• 比例は、 定義５ー６ による。
• 外項 とは、Ａ：Ｂ＝Ｃ：Ｄにおいて、Ａ、Ｄのことである。
  （以下、定義の補足（命題６ー１６） （外項）という。）
• 矩形は、 定義１ー２２ による。
• 内項 とは、Ａ：Ｂ＝Ｃ：Ｄにおいて、Ｂ、Ｃのことである。
  （以下、定義の補足２（命題６ー１６） （内項）という。）
• 等しいは、 公理１ー７ による。

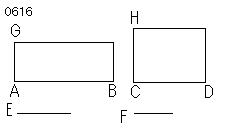
４線分ＡＢ、ＣＤ、Ｅ、Ｆが比例する、
　すなわち
　ＡＢがＣＤに対するように、
　ＥがＦに対する
　とせよ。

• 命題６ー１２（作図.比例第４項）
  による。
• 　ＡＢ、ＣＤ、Ｅ
  に対して、
  　線分Ｆ(;;ＡＢ：ＣＤ＝Ｅ：Ｆ)
  をとっている。

ＡＢ、Ｆにかこまれた矩形は
　ＣＤ、Ｅにかこまれた矩形に等しい
　と主張する。

点Ａ、Ｃから
　線分ＡＢ、ＣＤに直角に
　ＡＧ、ＣＨがひかれ、 【・・・(a)】

• 命題１ー１１（作図・線分からの垂線）
  による。
• 　Ｇ[;;ＡＧ⊥ＡＢ]、
  　Ｈ[;;ＣＨ⊥ＣＤ]
  をとっている。

　 ＡＧがＦに等しく、
　ＣＨがＥに等しくされた
　とせよ。 【・・・(b)】

• 命題１ー３の補足（作図.等しい線分となる点）
  により、
  　Ｇ'をＡＧ上に
  　ＡＧ'がＦに等しくなるようにとり、
  　Ｇ'を改めてＧとして
  　溯って用いている。
  Ｈについても同様である。
• 　Ｇ'(ＡＧ;;ＡＧ'＝Ｆ)、
  　Ｈ'(ＡＨ;;ＡＨ'＝Ｅ)
  をとり、
  　Ｇ'＞＞Ｇ、
  　Ｈ'＞＞Ｈ
  としている。

そうすれば
　ＡＢがＣＤに対するように、
　ＥがＦに対し、

• 命題の設定 による。
• 　ＡＢ：ＣＤ＝Ｅ：Ｆ
  となっている。

　ＥはＣＨに、
　ＦはＡＧに等しいから、

• (b)による。
• 　Ｅ＝ＣＨ、
  　Ｆ＝ＡＧ
  となっている。

　ＡＢがＣＤに対するように、
　ＣＨがＡＧに対する。

• 命題５ー１１の補足２（等しい量は同じ比をもつ）、
  命題５ー１１（同一の比に同じ比）
  による。
• 　ＡＢ：ＣＤ＝ＣＨ：ＡＤ
  となっている。

それゆえ
　平行四辺形ＢＧ、ＤＨの
　等しい角をはさむ辺は
　反比例する。

• 定義６ー２（逆比例）
  による。
• 　(ＡＢ,ＡＤ)(反比例)(ＣＤ,ＣＨ)
  となっている。
  

ところが
　等しい角をはさむ辺が反比例する
　等角な２つの平行四辺形は
　等しい。

• 命題６ー１４（等積で等角な平行四辺形と逆比例）
  である。

ゆえに
　 平行四辺形ＢＧは
　平行四辺形ＤＨに等しい。 【・・・(1)】

• 　平四ＢＧ＝平四ＤＨ
  となっている。

そして
　ＡＧはＦに等しいから、

• (b) による。
• 　ＡＧ＝Ｆ
  となっている。

　 ＢＧは矩形ＡＢ、Ｆである。 【・・・(2)】

• 定義１ー２２（正方形・矩形・菱形・長斜方形・トラペジオン）
  による。
• 　平四ＢＧ＝矩形(ＡＢ,Ｆ)
  となっている。

そして
　ＥはＣＨに等しいから、

• (b) による。
• 　Ｅ＝ＣＨ
  となっている。

　ＤＨは矩形ＣＤ、Ｅである。

• 定義１ー２２（正方形・矩形・菱形・長斜方形・トラペジオン）
  による。
• 　平四ＤＨ＝矩形(ＣＤ,Ｅ)
  となっている。

したがって、
　ＡＢ、Ｆにかこまれた矩形は
　ＣＤ、Ｅにかこまれた矩形に等しい。

• (1),(2), 公理１ー１の補足（等しいものに等しい）
  による。
• 　矩形(ＡＢ,Ｆ)＝矩形(ＣＤ,Ｅ)
  となっている。

次に
　ＡＢ、Ｆにかこまれた矩形が
　ＣＤ、Ｅにかこまれた矩形に等しい
　とせよ。

• 本命題の前半により
  　作図可能であるが、
  　その作図を前提にして、
  　論証するものではない。
  　矩形(ＡＢ,Ｆ)、ＣＤ
  に対して、
  　線分Ｅ[;;ＡＢ：ＣＤ＝Ｅ：Ｆ]、
  　矩形(ＣＤ,Ｅ)
  をとっている。
• 　矩形(ＡＢ,Ｆ)
  に対して、
  　矩形(ＣＤ,Ｅ;;矩形(ＣＤ,Ｅ)＝矩形(ＡＢ,Ｆ))
  をとっている。

４線分は
　比例する、
　すなわち
　ＡＢがＣＤに対するように、
　ＥがＦに対するであろう
　と主張する。

同じ作図がなされたとき、

• (a) (b) による。
• 　Ｇ[;;ＡＧ⊥ＡＢ]、
  　Ｈ[;;ＣＨ⊥ＣＤ]
  　Ｇ'(ＡＧ;;ＡＧ'＝Ｆ)、
  　Ｈ'(ＡＨ;;ＡＨ'＝Ｅ)、
  　Ｇ'＞＞Ｇ、
  　Ｈ'＞＞Ｈ
  をとっている。

　矩形ＡＢ、Ｆは
　矩形ＣＤ、Ｅに等しく、

• 命題の設定 による。
• 　矩形(ＡＢ,Ｆ)＝矩形(ＣＤ,Ｅ)
  となっている。

　ＡＧはＦに等しいから、

• (b)による。
• 　ＡＧ＝Ｆ
  となっている。

　矩形ＡＢ、ＦはＢＧである。

• 定義１ー２２（正方形・矩形・菱形・長斜方形・トラペジオン）
  による。
• 　矩形(ＡＢ,Ｆ)＝平四ＢＧ
  となっている。

そして
　ＣＨはＥに等しいから、

• (b)による。
• 　ＣＨ＝Ｅ
  となっている。

　矩形ＣＤ、ＥはＤＨである。

• 定義１ー２２（正方形・矩形・菱形・長斜方形・トラペジオン）
  による。
• 　矩形(ＣＤ,Ｅ)＝平四ＤＨ
  となっている。

それゆえ
　ＢＧはＤＨに等しい。

• 公理１ー１の補足（等しいものに等しい）
  による。
• 　平四ＢＧ＝平四ＤＨ
  となっている。

しかも
　等角である。

• 定義の補足（命題４ー２）(等角)
  による。
• 　∠ＧＡＢ＝∠ＨＣＤ
  となっている。

ところが
　等しくてかつ等角な２つの平行四辺形の
　等しい角をはさむ辺は
　反比例する。

• 命題６ー１４（等積で等角な平行四辺形と逆比例）
  による。
• 　(ＧＡ,ＡＢ)(反比例)(ＨＣ,ＣＤ)
  となっている。

ゆえに
　ＡＢがＣＤに対するように、
　ＣＨがＡＧに対する。

• 　定義６ー２（逆比例） による。
• 　ＡＢ：ＣＤ＝ＣＨ：ＡＧ
  となっている。

ところが
　ＣＨはＥに、
　ＡＧはＦに等しい。

• (b)による。
• 　ＣＨ＝Ｅ、
  　ＡＧ＝Ｆ
  となっている。

したがって
　ＡＢがＣＤに対するように、
　ＥがＦに対する。

• 命題５ー７（同一量の比）、
  命題５ー１１（同一の比に同じ比）
  による。
• 　ＡＢ：ＣＤ＝Ｅ：Ｆ
  となっている。

よってもし
　４線分が比例するならば、
　外項にかこまれた矩形は
　内項にかこまれた矩形に等しい。
そしてもし
　外項にかこまれた矩形が
　内項にかこまれた矩形に等しいならば、
　４線分は比例するであろう。
これが証明すべきことであった。

• 　線分ＡＢ上に、
  　矩形ＣＤ、ＤＦと等しい
  　矩形ＡＢ、ＢＣをつくる
  ことができる。
  (以下、命題６ー１６の補足３ (作図.線分上に矩形と等しい矩形)という。)
  なぜなら、
  　命題６ー１２（作図.比例第４項）
  により、
  　ＡＢ：ＣＤ＝ＤＦ：ＢＣ
  となるＢＣをもとめ、
  　命題２ー１の補足（作図.矩形）
  により
  　矩形ＡＢ、ＢＣをつくる
  ことができるから。
• 命題６ー１６は、
  　ＡＢ、ＣＤ、Ｅ
  に対して、
  　線分Ｆ(;;ＡＢ：ＣＤ＝Ｅ：Ｆ)、
  をとれば、
  　矩形(ＡＢ,Ｆ)＝矩形(ＣＤ,Ｅ)
  となり、
  　ＡＢ、ＣＤ、Ｅ
  に対して、
  　矩形(ＡＢ,Ｆ)＝矩形(ＣＤ,Ｅ)
  をとれば、
  　ＡＢ：ＣＤ＝Ｅ：Ｆ
  のことである。
  
• 命題６ー１６は推論用命題である。

  前提	作図	推論
  定義		1-22,補(題4-2),6-2
  公準
  公理		1-1補
  命題	1-3補,1-11,6-12	5-7,5-11,5-11補2,6-14
  その他

前 　　 次 　　 目次 　　頁頭