ユークリッド原論をどう読むか（１２）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第８巻
　
命題８ー１（順次比例の外項が互に素なら最小）
順次に比例
もし
　順次に比例する任意個の数があり、
　それらの外項が互いに素である
ならば、
　これらの数は
　それらと同じ比をもつ数のうち最小
である。

• 順次に比例 は、
  定義７ー２１（比例）により、
  任意個の数において、
  順次、前者と後者が同じ比をもつ
  ことである。
  (以下、定義の補足（命題８ー１） （順次に比例）という。)
  
• 数は、 定義７ー２による。
• 外項は、 定義の補足（命題６ー１６）による。
• 互いに素は、 定義７ー１３による。
• 同じ比は、 定義５ー５による。
• 最小は、 定義の補足３（命題３ー７）による。

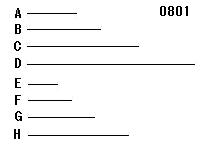
　順次に比例する
　任意個の数Ａ、Ｂ、[Ｃ₁、…、Ｃ_k、…、]Ｃ、Ｄがある

• 準一般的な証明である。
  コメント２（命題５ー１） 参照のこと。
• 「数（について）・・・とせよ」は、
  コメント４（命題７ー１）、
  同じ比をもつ線分の作図（仮想的）は、
  コメント２（命題５ー４）
  参照のこと。
• Ａ：Ｂ＝Ｂ：Ｃ₁＝…＝Ｃ_k：Ｃ_k+1＝…＝Ｃ：Ｄ
  となっている。
  

とし、
　その外項Ａ、Ｄが互いに素である
とせよ。

• 順次つながっている同じ比の
  　　最初Ａと最後Ｄが
  　外項である。
  本命題の例としては、
  　８：１２＝１２：１８＝１８：２７
  　とすればよい。
  確かに、
  　８と２７は
  　互いに素となっている。
  
• 　Ａ;(互いに素)Ｄ
  となっている。

　Ａ、Ｂ、[Ｃ₁、…、Ｃ_k、…、]Ｃ、Ｄは
　それらと同じ比をもつ数のうち
　最小である
と主張する。

もし
　最小でない
ならば、

• 背理法の仮定を述べようとしている。

　Ｅ、Ｆ、[Ｇ₁、…、Ｇ_k、…、]Ｇ、Ｈが
　Ａ、Ｂ、[Ｃ₁、…、Ｃ_k、…、]Ｃ、Ｄより小さく、
　しかも
　それらと同じ比をなす
とせよ。

• 背理法の仮定である。
• 　Ｅ：Ｆ＝Ａ：Ｂ、
  　Ｅ：Ｆ＝Ｆ：Ｇ₁＝…＝Ｇ_k：Ｇ_k+1＝…＝Ｇ：Ｈ、
  　Ａ＞Ｅ
  となっている。

そうすれば
　Ａ、Ｂ、[Ｃ₁、…、Ｃ_k、…、]Ｃ、Ｄは
　Ｅ、Ｆ、[Ｇ₁、…、Ｇ_k、…、]Ｇ、Ｈと同じ比をなし、
　Ａ、Ｂ、[Ｃ₁、…、Ｃ_k、…、]Ｃ、Ｄの個数は
　Ｂ、Ｆ、[Ｇ₁、…、Ｇ_k、…、]Ｇ、Ｈの個数に等しい
から、
　等間隔比により
　ＡがＤに対するように
　ＥがＨに対する。

• 　命題７ー１４（数の等間隔比） による。
• 　Ａ：Ｄ＝Ｅ：Ｈ
  となっている。

ところが
　Ａ、Ｄは［互いに］素であり、

• 命題の設定である。

　［互いに］素であるものは最小であり、
　最小の数は同じ比をもつ数を 割り切り、
　大きい数が大きい数を、
　小さい数が小さい数を、
　すなわち
　前項が前項を、
　後項が後項を割り切り、
　その商は等しい。

• 命題７ー２１（互いに素な数は同じ比の最小） 、
  命題７ー２０（同じ比なら最小のが割り切る）
  による。

それゆえ
　ＡはＥを割り切る、
　すなわち
　大きい数が小さい数を割り切る。

• 背理法の仮定による。
• 　Ａ｜Ｅ
  となっている。

　これは不可能である。

• 定義５ー１の補足２（割り切る） による。

ゆえに
　Ａ、Ｂ、[Ｃ₁、…、Ｃ_k、…、]Ｃ、Ｄより小さい
　Ｅ、Ｆ、[Ｇ₁、…、Ｇ_k、…、]Ｇ、Ｈは
　それらと同じ比をなさない。

• 背理法による。

したがって
　Ａ、Ｂ、[Ｃ₁、…、Ｃ_k、…、]Ｃ、Ｄは
　それらと同じ比をもつ数のうち最小である。

• 　Ａ：Ｂ＝Ｂ：Ｃ[₁＝…＝Ｃ_k：Ｃ_k+1＝…]＝Ｃ：Ｄ(最小)
  となっている。

　これが証明すべきことであった。

• 命題８ー１は、
  　Ａ：Ｂ＝Ｂ：Ｃ₁＝…＝Ｃ_k：Ｃ_k+1＝…＝Ｃ：Ｄ、
  　Ａ;(互いに素)Ｄ
  ならば、
  　Ａ：Ｂ＝Ｂ：Ｃ₁＝…＝Ｃ_k：Ｃ_k+1＝…＝Ｃ：Ｄ(最小)
  のことである。
• 命題８ー１は推論用命題である。

  前提	作図	推論
  定義		5-1補2
  公準
  公理
  命題		7-14,7-20,7-21
  その他	コ2(題5-4),コ4(題7-1)	背理法, コ2(題5-1)

前 　　 次 　　 目次 　　頁頭