ユークリッド原論をどう読むか（１０）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第６巻

命題６ー３３（弧と中心角・円周角の比例）
等しい２円において
　角は
　中心角も円周角も
　それらが立つ弧と同じ比をもつ。

• 等しいは、 定義３ー１ による。
• 円は、 定義１ー１５ による。
• 角は、 定義１ー８ による。
• 中心角は、 定義の補足２（命題３ー２０） による。
• 円周角は、 定義の補足３（命題３ー２０） による。
• 立つは、 定義３ー９ による。
• 弧は、 定義１ー１８の補足 による。
• 同じ比は、 定義５ー５ による。

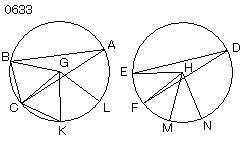
ＡＢＣ、ＤＥＦを等しい円とし、
　角ＢＧＣ、ＥＨＦを
　それらの中心Ｇ、Ｈにおける角とし、
　角ＢＡＣ、ＥＤＦを
　円周における角とせよ。

• 　円ＡＢＣ[;;(Ａ,Ｂ,Ｃ);上.円周ＡＢＣ]
  に対して、
  　命題３ー１（作図.円の中心）
  により、
  　中心Ｇ.円ＡＢＣ
  をとり、
  　公準１ー１の補足（作図.任意の点をとる）
  により、
  　点Ｈ
  をとり、
  　命題１ー２（作図・線分）
  により、
  　線分ＨＤ[;;＝ＧＡ]
  をとり、
  　公準１ー３（作図.円）
  により、
  　円ＤＥＦ(Ｈ,ＨＤ;;(Ｄ,Ｅ,Ｆ);上.円周ＤＥＦ)
  をとると、
  　円ＡＢＣ＝円ＤＥＦ
  となっている。
  
• 　円ＡＢＣ[;;(Ａ,Ｂ,Ｃ);上.円ＡＢＣ]
  に対して、
  　中心Ｇ.円ＡＢＣ、
  　点Ｈ、
  　円ＤＥＦ(Ｈ,;;＝円ＡＢＣ,(Ｄ,Ｅ,Ｆ);上.円ＤＥＦ)、
  をとっている。

弧ＢＣが弧ＥＦに対するように、
　角ＢＧＣが角ＥＨＦに、
　角ＢＡＣが角ＥＤＦに対する
　と主張する。
　
任意個のＣＫ、ＫＬが
　次々に弧ＢＣに等しくされ、

• 公準１ー１（作図.直線）
  により
  　弦ＢＣを結ぶ。
  命題４ー１（作図.線分の挿入）
  により
  　点Ｋ(円ＡＢＣ,外.Ｂ;;ＣＫ＝(挿入)ＢＣ)
  をとっている。 このとき、
  　命題３ー２８（等しい弦は等しい弧を切り取る）
  により
  　弧ＢＣ＝弧ＣＫ。
  必要な回数だけ
  　この操作を繰り返せばよい。
  
• 準一般的な証明は、
  　コメント２（命題５ー１）参照のこと。
  命題５ー１（同数倍の和１）
  と同様に補足すれば、
  　一般的な証明となる。
  
• 　弧ＣＫ＝弧ＢＣ
  　弧ＫＬ＝弧ＢＣ
  　・・・
  となっている。

　任意個のＦＭ、ＭＮが
　弧ＥＦに等しくされ、

• 上と同様である。
  ただし、
  　倍数（回数）は上と独立である。
  
• 　弧ＦＭ＝弧ＥＦ、
  　弧ＭＮ＝弧ＥＦ
  をとっている。

　ＧＫ、ＧＬ、ＨＭ、ＨＮが結ばれたとせよ。

• 公準１ー１（作図.直線）
  による。
• 　半径ＧＫ、ＧＬ、ＨＭ、ＨＮ
  をとっている。

　
そうすれば
　弧ＢＣ、ＣＫ、ＫＬは
　互いに等しいから、

• 　弧ＢＣ＝ＣＫ＝ＫＬ
  となっている。

　角ＢＧＣ、ＣＧＫ、ＫＧＬは
　互いに等しい。

• 命題３ー２７（弧が等しければ角も等しい）
  による。
• 　∠ＢＧＣ＝∠ＣＧＫ＝∠ＫＧＬ
  となっている。

それゆえ
　弧ＢＬがＢＣの何倍であろうと、
　角ＢＧＬは
　角ＢＧＣの同じ倍数である。

• 　(弧ＢＬ、∠ＢＧＬ)＝ｍ(弧ＢＣ、∠ＢＧＣ)
  となっている。

同じ理由で
　弧ＮＥが弧ＥＦの何倍であろうと、
　角ＮＨＥは
　角ＥＨＦの同じ倍数である。

• 角ＢＧＬの倍数とＮＥＨの倍数とは
  　独立である。
  
• 　(弧ＮＥ、∠ＮＥＨ)＝ｎ(弧ＥＦ、∠ＥＨＦ)
  となっている。

《ゆえに》［ところが］もし
　弧ＢＬが弧ＥＮに等しければ、
　角ＢＧＬも角ＥＨＮに等しく、
　もし
　弧ＢＬが弧ＥＮより大きければ、
　角ＢＧＬも角ＥＨＮより大きく、
　もし
　小さければ、小さい。 【・・・(1)】

• 論証の流れからすると、
  　「ところが」という雰囲気がふさわしい。
  「ゆえに」はなじまない。
  
• 命題３ー２７（弧が等しければ角も等しい）、
  公理１ー８（大きい）、
  公理１ー８の補足（小さい）
  による。
• 　弧ＢＬ(＜,＝,＞)弧ＥＮ
  ならば
  　∠ＢＧＬ(＜,＝,＞)∠ＥＨＮ
  となっている。

そこで
　４つの量、
　２つは弧ＢＣ、ＥＦ、
　２つは角ＢＧＣ、ＥＨＦがあり、
　弧ＢＣ、角ＢＧＣの同数倍なる
　弧ＢＬ、角ＢＧＬと、
　弧ＥＦ、角ＥＨＦの同数倍なる
　弧ＥＮ、角ＥＨＮとがとられている。

• 定義５ー５（同じ比）
  にしたがって
  　同じ比であることを
  　論証するための前提を
  　確認している。
  
• 　(弧ＢＬ、∠ＢＧＬ)＝ｍ(弧ＢＣ、∠ＢＧＣ)、
  　(弧ＥＮ、∠ＥＨＮ)＝ｎ(弧ＥＦ、∠ＥＨＦ)
  となっている。

そしてもし、
　弧ＢＬが弧ＥＮより大きければ、
　角ＢＧＬも角ＥＨＮより大きく、
　等しければ、等しく、
　小さければ小さい
　ことが証明された。

• (1) による。
• 　弧ＢＬ(＜,＝,＞)弧ＥＮ
  ならば
  　∠ＢＧＬ(＜,＝,＞)∠ＥＨＮ
  となっている。

したがって
　弧ＢＣがＥＦに対するように、
　角ＢＧＣが角ＥＨＦに対する。

• 定義５ー５（同じ比）
  による。
• 　弧ＢＣ：弧ＥＦ＝∠ＢＧＣ：∠ＥＨＦ
  となっている。

《ところが》［また］
　角ＢＧＣが角ＥＨＦに対するように、
　角ＢＡＣが角ＥＤＦに対する。
なぜなら
　どちらも２倍であるから。

• ここは、
  　中心角に続けて、
  　円周角についての論証であり、
  　「また」の方が妥当である。
  
• 命題５ー１５（同数倍の比）
  による。
• 「なぜなら・・・であるから」は、
  　コメント２（命題１ー１６）参照のこと。
• 　∠ＢＧＣ：∠ＥＨＦ＝∠ＢＡＣ：∠ＥＤＦ
  となっている。

それゆえ
　弧ＢＣが弧ＥＦに対するように、
　角ＢＧＣが角ＥＨＦに、
　角ＢＡＣが角ＥＤＦに対する。

• 　命題５ー１１（同一の比に同じ比）
  による。
• 　弧ＢＣ：弧ＥＦ
  　＝∠ＢＧＣ：∠ＥＨＦ
  　＝∠ＢＡＣ：∠ＥＤＦ
  となっている。

よって
　等しい２円において
　角は
　中心角も円周角も
　それらが立つ弧と同じ比をもつ。
これが証明すべきことであった。

• 直線図形以外の比例の初出である。
• 命題６ー３３は、
  　円ＡＢＣ[Ｇ,ＧＡ;;(Ｂ,Ｃ);上.円ＡＢＣ]
  に対して、
  　円ＤＥＦ(Ｈ,;;＝円ＡＢＣ,(Ｄ,Ｅ,Ｆ);上.円ＤＥＦ)、
  をとれば、
  　弧ＢＣ：弧ＥＦ
  　＝∠ＢＧＣ：∠ＥＨＦ　(中心角)
  　＝∠ＢＡＣ：∠ＥＤＦ　(円周角)
  のことである。
  
• 命題６ー３３は推論用命題である。

  前提	作図	推論
  定義		5-5
  公準	1-1,1-1補,1-3
  公理		1-8,1-8補
  命題	1-2,3-1,4-1	3-27,3-28,5-11,5-15
  その他		コ2(題1-16),コ2(題5-1)

前 　　 次 　　 目次 　　頁頭