ユークリッド原論をどう読むか（７）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第３巻

命題３ー２０（中心角は円周角の２倍）　
底辺 　 中心角 　 円周角

円において
　角が
　同じ弧を底辺とするとき、
中心角は
　円周角の２倍である。

• 円は、 定義１ー１５ による。
• 角は、 定義１ー８ による。
• 弧は、 定義１ー１８の補足 による。
• 底辺は、
  　 定義１ー２０の補足２ にあるが、
  ここでは、
  　円周上の点と
  　弧の両端とを結んでできる
  　　図形を
  　三角形に見立てて、
  　中心角、円周角の対辺となる
  　弧の部分を
  　底辺と
  　呼んでいる。
  以下、
  　定義の補足（命題３ー２０）(底辺)という。
• 中心角は、
  　弧の両端と
  　中心とを結んでできる
  　　２つの半径のなす角である。
  以下、定義の補足２（命題３ー２０）(中心角)という。
• 円周角は、
  　弧の両端と
  　円周上の点とを結んでできる
  　　２つの弦のなす角である。
  以下、
  　定義の補足３（命題３ー２０）(円周角)という。
• 倍は、 定義の補足（公理１ー５） による。

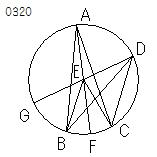
ＡＢＣを円とし、
　ＢＥＣをその中心角、

• Ｅは、 命題３ー１ （作図.円の中心）
  による。
• 公準１ー１ （作図.直線）
  
• 　円ＡＢＣ
  に対して、
  　中心Ｅ.円ＡＢＣ、
  　点Ｂ[円周ＡＢＣ]、
  　点Ｃ[円周ＡＢＣ;;Ｃ;外.Ｂ]、
  　∠ＢＥＣ;中心角.円ＡＢＣ
  となっている。

　ＢＡＣを円周角とし、
　それらが
　同じ弧ＢＣを底辺とするとせよ。

• 　点Ａ[円周ＡＢＣ;;Ａ;(外.Ｂ、外.Ｃ)]、
  　∠ＢＡＣ;円周角.円ＡＢＣ
  となっている。

角ＢＥＣは
　角ＢＡＣの２倍である
　と主張する。
　
ＡＥが結ばれ、

• 公準１ー１ （作図.直線）
  
• 　線分ＡＥ
  をとっている。 による。
  

　Ｆまで延長されたとせよ。

• 公準１ー２ （作図.直線の延長）
  により、
  　半径ＡＥをＥの方向に延長する。
  Ｅは
  　円の内部の点であるから、
  延長した部分は
  　 命題３−２の補足 (円内通過直線は円周と２交点)
  により、
  　円周と１点で交わる。
  その交点をＦとする。
  
• 　交点Ｆ(延長ＡＥ.円周ＡＢＣ)
  をとっている。
  
• Ｆは、
  　弧ＢＣ上にある場合と、
  　弧ＣＡ上にある場合、
  　弧ＢＡ上にある場合
  　がある。
  

[弧ＢＣ上にある場合]
そうすれば
ＥＡは
　ＥＢに等しいから、

• 命題の設定 , 定義１ー１５ （円）
  による。
• 　ＥＡ＝ＥＢ
  となっている。

　角ＥＡＢも
　角ＥＢＡに等しい。

• 命題１ー５ （２等辺三角形の底角）
  による。
• 　∠ＥＡＢ＝∠ＥＢＡ
  となっている。

それゆえ
角ＥＡＢ、ＥＢＡの和は
　角ＥＡＢの２倍である。

• 定義の補足（公理１ー５） （同じもののｎ倍）
  による。
• 　∠ＥＡＢ＋∠ＥＢＡ＝２∠ＥＢＡ
  となっている。

ところが
角ＢＥＦは
　角ＥＡＢ、ＥＢＡの和に等しい。

• 命題１ー３２ （三角形の内対角・内角の和）
  による。
• 　∠ＢＥＦ＝∠ＥＡＢ＋∠ＥＢＡ
  となっている。

ゆえに
　角ＢＥＦも
　角ＥＡＢの２倍である。 【・・・(1)】

• 公理１ー１の補足 （等しいものに等しい）
  による。
• 　∠ＢＥＦ＝２∠ＥＡＢ
  となっている。

同じ理由で
　角ＦＥＣも
　角ＥＡＣの２倍である。

• 　∠ＦＥＣ＝２∠ＥＡＣ
  となっている。

したがって
角ＢＥＣ全体は
　角ＢＡＣ全体の２倍である。

• (1) 公理１ー７ （等しい）
  による。
• 　∠ＢＥＣ＝２∠ＢＡＣ
  となっている。

　
[弧ＣＡ上にある場合]
もう１度
　線分が折り曲げられ《たとし》［て］、
　別の角ＢＤＣがあるとし、

• Euclid's Elements
  　（Clark University Professor D.E.Joyce
  の英文では、
  Again, let another straight line be inflected, and let there be another angle BDC.
  となっている。
• 前半の例で言えば、
  　Ｆが弧ＡＢ上にある場合である。
• 　点Ｄ[内.弧ＡＣ,同側(ＥＢ,Ｃ)]
  をとっている。

　ＤＥが結ばれ、

• 公準１ー１ （作図.直線）
  による。
• 　線分ＤＥ
  をとっている。

　Ｇまで延長されたとせよ。

• 公準１ー２ （作図.直線の延長）
  により、
  　ＤＥが
  　Ｅの方向に延長される。
  前半と同様の理由により
  延長した部分は
  　円周と１点で交わる。
  その点をＧとする。
  Ｇは
  　弧ＣＡ上にある。
• 　交点Ｇ(延長ＤＥ,弧ＡＢ)
  をとっている。

同様にして
角ＧＥＣは
　角ＥＤＣの２倍であり、
　そのうち
ＧＥＢは
　ＥＤＢの２倍である。
それゆえ
残りのＢＥＣは
　［残りの］ＢＤＣの２倍である。

• 公理１ー７ （等しい）
  による。
• 　∠ＧＥＣ＝２∠ＥＤＣ、
  　∠ＧＥＢ＝２∠ＥＤＢ、
  　∠ＢＥＣ＝２∠ＢＤＣ
  となっている。

[弧ＢＡ上にある場合
　も同様である。］
よって
［３つの場合の結果により］
　円において
　角が
　同じ弧を底辺とするとき、
中心角は
　円周角の２倍である。
これが証明すべきことであった。

• 命題３ー２０は、 　　円ＡＢＣ
  に対して、
  　中心Ｅ.円ＡＢＣ、
  　点Ｂ[円周ＡＢＣ]、
  　点Ｃ[円周ＡＢＣ;;Ｃ;外.Ｂ]、
  　∠ＢＥＣ;中心角.円ＡＢＣ、
  　点Ａ[内.弧ＢＣ]、
  　∠ＢＡＣ、
  をとれば、
  　∠ＢＥＣ＝２∠ＢＡＣ
  のことである。
• 命題３ー２０は推論用命題である。

  前提	作図	推論
  定義		1-15,補(理1-5)
  公準	1-1,1-2
  公理		1-1補,1-7
  命題	3-1,3-2補	1-5,1-32
  その他		場合分け

前 　　 次 　　 目次 　　頁頭