ユークリッド原論をどう読むか（９515）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第５巻

命題５ー１５（同数倍の比）
約量は
　同順にとられたとき、
　それらの同数倍と同じ比をもつ。

• 約量は、定義５ー１ による。
• 同数倍は、定義５ー５の補足 による。
• 同じ比は、定義５ー５ による。

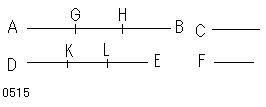
ＡＢはＣの、
　ＤＥはＦの
　同数倍とせよ。

• 　量Ｃ、Ｆ、個数ｍ
  をとり、
  　ＡＢ＝ｍＣ、ＤＥ＝ｍＦ
  をとっている。

ＣがＦに対するように、
　ＡＢがＤＥに対する
　と主張する。
　
ＡＢはＣの、
　ＤＥはＦの
　同数倍であるから、

• 命題の設定 である。
• 　(ＡＢ、ＤＥ)＝ｍ(Ｃ、Ｆ)
  となっている。

ＡＢのなかにある
　Ｃに等しい量と同じ個数の、
　Ｆに等しい量が
　ＤＥの中にある。

• 　個数(ＡＢ,Ｃ)＝個数(ＤＥ,Ｆ)＝ｍ
  となっている。

ＡＢが
　Ｃに等しいＡＧ、ＧＨ、[ＨiＨ'i、]ＨＢに、
　ＤＥが
　Ｆに等しいＤＫ、ＫＬ、[ＬiＬ'i、]ＬＥに
　分けられたとせよ。【・・・(a)】

• 推論の設定である。
• 準一般的な証明である。
  コメント２（命題５ー１）を参照のこと。
  準一般的な証明の一般化の方法は、
  　コメント５（命題５ー１）
  　参照のこと。
• 　点Ｈ1＝点Ｇ(ＡＢ;;ＡＧ＝Ｃ)、
  　点Ｈi+1＝点Ｈ'i(ＡＢ;;ＨiＨ'i＝Ｃ)、
  　点Ｈn＝Ｂ、
  　点Ｌ1＝点Ｋ(ＤＥ;;ＤＫ＝Ｆ)、
  　点Ｌi+1＝点Ｌ'(ＤＥ;;ＬiＬ'i＝Ｆ)
  　点Ｌn＝Ｅ、
  をとっている。

そうすれば
　ＡＧ、ＧＨ、[ＨiＨ'i、]ＨＢと
　ＤＫ、ＫＬ、[ＬiＬ'i、]ＬＥとは
　同じ個数であろう。
そして
　ＡＧ、ＧＨ、[ＨiＨ'i、]ＨＢは互いに等しく、
　ＤＫ、ＫＬ、[ＬiＬ'i、]ＬＥも互いに等しいから、

• (a) による。
• 　ＡＧ＝ＧＨ＝[ＨiＨ'i＝]ＨＢ＝Ｃ、
  　ＤＫ＝ＫＬ＝[ＬiＬ'i＝]ＬＥ＝Ｆ
  となっている。

　ＡＧがＤＫに対するように、
　ＧＨはＫＬに、
［ＨiＨ'iはＬiＬ'iに、］
　ＨＢはＬＥに対する。【・・・(1)】

• 命題５ー１１の補足２（等しい量は同じ比をもつ）
  による。
• 　ＡＧ：ＤＫ＝ＨiＨ'i：ＬiＬ'i
  となっている。

それゆえ
　前項の１つが後項の１つに対するように、
　前項の総和が後項の総和に対するであろう。

• 命題５ー１２（比例する前項の和と後項の和）
  のことである。

ゆえに
　ＡＧがＤＫに対するように、
　ＡＢがＤＥに対する。【・・・(2)】

• (1) ,命題５ー１２（比例する前項の和と後項の和）
  による。
• 　ＡＧ：ＤＫ＝ＡＢ：ＤＥ
  となっている。

しかも
　ＡＧはＣに、
　ＤＫはＦに等しい。

• (a) による。
• 　ＡＧ＝Ｃ、ＤＫ＝Ｆ
  となっている。

したがって
　ＣがＦに対するように、
　ＡＢがＤＥに対する。

• (2) ,命題５ー１１の補足２（等しい量は同じ比をもつ） 、
  命題５ー１１（同一の比に同じ比）
  による。
• 　Ｃ：Ｆ＝ＡＢ：ＤＥ
  となっている。

よって
　約量は
　同順にとられたとき、
　それらの同数倍と同じ比をもつ。
これが証明すべきことであった。

• 命題５ー１５は、
  　Ｃ：Ｆ＝ｍＣ：ｍＦ
  のことである。
• 命題５ー１５は推論用命題である。

  前提	作図	推論
  定義
  公準
  公理
  命題		5-11,5-11補2,5-12
  その他		コ2(題5-1),コ5(題5-1)

前 　　 次 　　 目次 　　頁頭