ユークリッド原論をどう読むか（７）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第３巻

命題３ー２８（等しい弦は等しい弧を切り取る）

等しい円において
等しい弦は
　等しい弧を切り取る、
　すなわち
切り取られた大きい弧は
　大きい弧に、
小さい弧は
　小さい弧に等しい。
　

• 等しいは、 公理１ー７ による。
• 円は、 定義１ー１５ による。
• 弦は、 定義３ー４の補足 による。
• 弧は、 定義１ー１８の補足 による。
• 等しいは、 公理１ー７ による。
• 大きいは、 公理１ー８ による。
• 小さいは、 公理１ー８の補足 による。

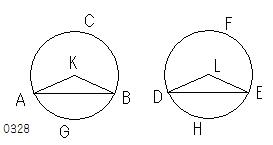
ＡＢＣ、ＤＥＦを
　等しい円とし、
　それらの円において
　ＡＢ、ＤＥを等しい弦とし、
これが
　大きい弧ＡＣＢ、ＤＦＥと
　小さい弧ＡＧＢ、ＤＨＥ
　を切り取るとせよ。

• 　円ＡＢＣ
  に対して、
  　中心Ｋ.円ＡＢＣ、
  　点Ａ[円周.ＡＢＣ]、
  　点Ｂ[円周.ＡＢＣ,外.Ａ]、
  　点Ｌ[]、
  　円ＤＥＦ(Ｌ,ＫＡ)、
  　点Ｄ[上.円周ＤＥＦ]、
  　点Ｅ(上.円ＤＥＦ,同向側(ＤＬ,ＡＫ,Ｂ);;ＤＥ＝ＡＢ)
  をとっている。

大きい弧ＡＣＢは
　大きい弧ＤＥＦに、
小さい弧ＡＧＢは
　小さい弧ＤＨＥに等しいと主張する。 円の中心Ｋ、Ｌがとられ、

• 命題３ー１ （作図.円の中心）
  による。
• 　中心Ｋ.円ＡＢＣ、
  　中心Ｌ.円ＤＥＦ
  となっている。

　ＡＫ、ＫＢ、ＤＬ、ＬＥが
　結ばれたとせよ。

• 公準１ー１ （作図.直線）
  による。
• 　線分ＡＫ、ＫＢ、ＤＬ、ＬＥ
  をとっている。

　 そうすれば
２つの円は
　等しいから、
半径も
　等しい。

• 定義３ー１ （等しい２円）
  による。
• 　ＡＫ＝ＤＬ
  となっている。

かくて
２辺ＡＫ、ＫＢは
　２辺ＤＬ、ＬＥに等しい。
そして
底辺ＡＢは
　底辺ＤＥに等しい。

• 命題の設定 による。
• 　(ＡＫ、ＫＢ)＝(ＤＬ、ＬＥ)
  　ＡＢ＝ＤＥ
  となっている。

それゆえ
　角ＡＫＢは
　角ＤＬＥに等しい。

• 命題１ー８ （３辺相等２）
  による。
• 　∠ＡＫＢ＝∠ＤＬＥ
  となっている。

ところが
等しい角は
　中心においてあるとき、
　等しい弧の上にたつ。

• 命題３ー２６ （角が等しければ弧は等しい）
  による。

ゆえに
弧ＡＧＢは
　ＤＨＥに等しい。 【・・・(1)】

• 　弧ＡＧＢ..円ＡＢＣ(∠ＡＫＢ)
  　≡弧ＤＨＥ..円ＤＥＦ(∠ＤＬＥ)
  となっている。

また
円ＡＢＣ全体も
　円ＤＥＦ全体に等しい。

• 命題の設定 による。
• 　円ＡＢＣ≡円ＤＥＦ
  となっている。

したがって
残りの弧ＡＣＢも
　残りの弧ＤＦＥに等しい。

• (1) , 公理１ー７ （等しい）
  による。
• 　弧ＡＣＢ..円ＡＢＣ(弧ＡＧＢ.円ＡＢＣ,対)
  　≡弧ＤＦＥ..円ＤＥＦ(弧ＤＨＥ.円ＤＥＦ,対)
  となっている。

よって
　等しい円において
等しい弦は
　等しい弧を切り取る、
　すなわち
　切り取られた
大きい弧は
　大きい弧に、
小さい弧は
　小さい弧に等しい。
　
これが証明すべきことであった。

• 命題３ー２８は、
  　円ＡＢＣ
  に対して、
  　円ＤＥＦ[;;＝円ＡＢＣ]、
  　弦ＤＥ..円ＤＥＦ[;;＝弦ＡＢ.円ＡＢＣ]
  をとれば、
  　弧ＤＨＥ..弦ＤＥ.円ＤＥＦ(反対側(ＤＥ,中心.円ＤＥＦ))
  　≡弧ＡＧＢ..弦ＡＢ.円ＡＢＣ(反対側(ＡＢ,中心.円ＡＢＣ))、
  　弧ＤＦＥ..円ＤＥＦ(弧ＤＨＥ.円ＤＥＦ,対)
  　≡弧ＡＣＢ..円ＡＢＣ(弧ＡＧＢ.円ＡＢＣ,対)
  のことである。
• 命題３ー２８は推論用命題である。

  前提	作図	推論
  定義		3-1
  公準	1-1
  公理		1-7
  命題	3-1	1-8 ,3-26
  その他

前 　　 次 　　 目次 　　頁頭