ユークリッド原論をどう読むか（６）
頁末 　　 前 　　 次 　　 目次　

ユークリッド原論

第３巻

命題３ー１（作図.円の中心）　
(中心は弦の２等分線上)
(中心を通る直線は円周と２交点)
与えられた円の中心を
　見いだすこと。

• 円は定義１ー１５ による。
• 中心は定義１ー１６ による。

与えられた円を
　ＡＢＣとせよ。
このとき
円ＡＢＣの中心を
　見いださねばならぬ。



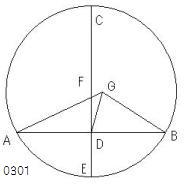
円を通って
　任意に線分ＡＢがひかれ、

• 定義１ー１５（円）から
  　円には内部に中心がある
  　ことを前提としている。
  論理的には
  　中心が具体的に求められなくても
  存在は
  　確保されている。
  しかし
  　中心が分からなくても
  　円が存在している
  　というのが原論の立場であるとみる。
  今日的には
  　中心の文字で円を示すが、
  原論においては、
  　円周上の３点の文字で円を示している
  　のもその現れである。
  したがって、可能な限り、
  　中心を具体的に求める
  　という姿勢が原論には見える。
  命題３ー２、命題３ー３（直径と弦）がそうである。
  そのために、
  　命題３ー１（作図.円の中心）で
  　中心が求まることを証明している。
• 円周上の２点を結ぶ線分が
  　円の内部にあることは、
  　定義１ー１５（円）により
  　中心の存在が確保されることによって、
  　本質的に本命題とは独立に、
  　次の命題３ー２（弦は円の内部）　 で証明される。
  したがって、
  　論理的には、
  　命題３ー２（弦は円の内部）　が前提となって、
  　命題３ー１ （作図.円の中心） が証明される方が
  　筋道が見やすい。
• 定義１ー１５（円） により
  　円周の一方の側は内部であり
  　他方の側は外部である。
  公準１ー１の補足（作図.任意の点をとる） により
  　円の内部と外部とにそれぞれ点をとり、
  　公準１ー１（作図.直線） により
  　この２点を結ぶ線分をひき、
  　公準１ー２（作図.直線の延長） により
  　延長すると、
  　内部の点から両側に延長されるので、
  　命題の補足３（定義１ー１４）（図形と直線の交点） により
  　円と少なくとも２点で交わる。
  この２点を、
  　改めてＡ、Ｂとする。

点Ｄにおいて２等分され、

• 命題１ー１０（作図・線分の２等分） による。
• ＡＢの中点Ｄが円の内部にあることは、証明済みではない。

ＤからＡＢに直角にＤＣがひかれ、 【・・・(a)】

• 命題１ー１１（作図・線分からの垂線） により
  　ＡＢに直角な直線を
  　Ｄから
  　直線ＡＢについて
  　円周上の点Ｃと同じ側にひくことができる。
  この直線が
  　円周と交わることについては、
  　証明済みではない。
  この直線は
  　ＡＢについて
  　Ｃ（Ａ、Ｂと異なる円周上の任意の点）と
  　同じ側にひいてあるので、
  　この上にＣ’をとっておく。
  Ｃ’が
  　円のどこにあるか
  　は確定できない。

Ｅまで延長され、

• 公準１ー２（作図.直線の延長） により
  　上にひいた直線を、
  　ＡＢについて
  　Ｃ’と異なる側に延長し、
  　延長した直線上に、
  　公準１ー１の補足（作図.任意の点をとる） により
  　Ｅをとっておく。
  Ｅが
  　円のどこにあるか
  　は確定できない。

［直線Ｃ’Ｅ上に
円ＡＢＣの中心が
　あり、
Ｃ’Ｅが
　２点で円と交わり、
　その２点を改めてＣ、Ｅとできたと仮定したとき］ 【・・・(Ａ)】
ＣＥが
　Ｆにおいて２等分されたとせよ。

• 命題１ー１０（作図・線分の２等分） による。

Ｆは
　ＡＢＣの中心である
　と主張する。

• Ｄが円の内部にあること、
  　線分ＣＥが円の内部にあること
  　は証明済みではない。
  この部分は
  　原論のギャップの一つであり、
  　交点等の存在を
  　とことん論理的に追究しきれなかった
  　　原論の特徴を
  　示している。

そうでないとすれば、

• 背理法の仮定である。

もし可能ならば

• 背理法の仮定であることを
  　繰り返し述べている。
• 「もし可能ならば」は、
  　 コメント２(命題１−７） (もし可能ならば)参照のこと。

［Ｃ’Ｅ上にない］
　Ｇを中心とすると、
定義１ー７の補足 により
　［ＧがＣ’Ｅについて
　 Ｂと同じ側にある場合と、
　 Ｂと反対側にある場合
　がある。
］
[ Ｂと同じ側にある場合、]
　ＧＡ、ＧＤ、ＧＢが
　結ばれたとせよ。 【・・・(b)】

• 公準１ー１（作図.直線） により
  　ＧとＡ、Ｄ、Ｂとを
  　それぞれ結んでいる。

そうすれば
ＡＤは
　ＤＢに等しく、

• (a) による。

ＤＧは
　共通であるから、
２辺ＡＤ、ＤＧは
　２辺《ＧＤ、ＤＢ》［ＢＤ、ＤＧ］に等しい。
そして
　半径であるから、
底辺ＧＡは
　底辺ＧＢに等しい。

• 定義１ー１５（円） による。

それゆえ
角ＡＤＧは
　角ＧＤＢに等しい。

• 命題１ー８（３辺相等２） による。

ところが
　直線の上に直線が立てられて
　接角を互いに等しくするとき、
等しい角の双方は
　直角である。

• 定義１ー１０（直角） である。

ゆえに
角ＧＤＢは
　直角である。
そして
角ＦＤＢも
　直角である。

• (a) による。

したがって
角ＦＤＢは
　角ＧＤＢに、
すなわち
大きいものが
　小さいものに等しい。

• Ｇが
  　Ｃ’Ｅについて
  　Ｂと同じ側にある
  すなわち
  　角Ｃ’ＤＢの内部にある
  　　という背理法の仮定(b) と
  　公理１ー８（大きい） とによる。　

これは不可能である。

［Ｇが
　Ｃ’Ｅについて
Ｂと反対側にある場合も、
　同様である。］

《したがって
Ｇは
　円ＡＢＣの中心ではない。

• 背理法による。

》 ［
したがって
２つの場合の結果から、
中心は
　Ｃ’Ｅ上にある。

• 背理法による。
• ここで、ようやく、証明の冒頭の設定(Ａ) が満たされたことになる。

中心Ｆは
　円の内部にあるから、

• 定義１ー１５（円） 、１ー１６（中心） による。

直線Ｃ’Ｅが
　円の内部を通る。
直線Ｃ’Ｅと円周との交点を
　改めてＣ、Ｅとする。

• 命題の補足３（定義１ー１４）（図形と直線の交点） によって、
  この直線は
  　円周と少なくとも２点で交わる。
  その交点を
  　改めてＣ、Ｅとしている。

線分ＣＥを
　２等分する点を改めてＦとすると、

• 命題１ー１０（作図・線分の２等分） による。

Ｆは
　円ＡＢＣの中心である。
なぜなら［もし］
中心が
　線分ＣＥ上で
　ＣＥの２等分点以外の点Ｇ’であるとすると、

• 背理法の仮定である。

Ｃ、Ｅは
　円周上の点であるので、
Ｇ’Ｃは
　Ｇ’Ｅに等しくなるが、

• 定義１−１５（円）、１ー１６（中心） による。

これは
Ｇ’が
　ＣＥの２等分点でないこと
　に矛盾する。
したがって
Ｆが
　中心である。

• 背理法による。

］ 同様にして
　Ｆ以外のいかなる点も
　中心でない
　ことを証明しうる。

• 原論の元来の論証過程に沿えば、
  　Ｇが
  　Ｃ’Ｅについて
  　Ｂと異なる側にある場合も
  　同様である
  　という意味である。
  この解説では、
  　補足しているので
  　不要になっている。
  なお、
  　コメント（命題１ー１４）(〜以外の)を参照のこと
  

よって
点Ｆは
　［円］ＡＢＣの中心である。

［３ー１］系
　
《これから》
［本命題の証明の中で前半で］
　次のことが明らかである、
すなわち
もし
　円において
　直線が弦を直角に２等分するならば、
円の中心は
　２等分線上にある。
　
［（以下、命題３−１の系(中心は弦の２等分線上)という。）］ これが証明すべきことであった。
　

• 円には
  中心は
  　１点しかなく、
  したがって
  半径は
  　すべて互いに等しいこと、
  しかも
  　中心が作図で確定できること
  　を主張している。
• 中心を通る直線は
  　円周と２点だけで交わり、
  　この２点を結ぶ線分が
  　定義１−１７（直径）により直径であって、
  中心は
  　直径を２等分する点である
  　こともわかる。
  　（以下、命題３−１の補足２(中心を通る直線は円周と２交点)という。）
• 命題３−１の系(中心は弦の２等分線上)は推論用命題である。

  前提	作図	推論
  定義		1-7補, 1-10, 1-15
  公準	1-1, 1-1補, 1-2
  公理		1-8
  命題	補3(義1-14), 1-10, 1-11	1-8
  その他		背理法

• 命題３−１の補足(中心を通る直線は円周と２交点)は推論用命題である。

  前提	作図	推論
  定義		1-17
  公準
  公理
  命題
  その他

• 命題３ー１は作図用命題である。

  前提	作図	推論
  定義		1-7補,1-10,1-15,1-16
  公準	1-1,1-1補,1-2
  公理		1-8
  命題	補3(義1-14),1-10,1-11	1-8
  その他		背理法, コ2(題1-7),場合分け,他の〜

前 　　 次 　　 目次 　　頁頭