ユークリッド原論をどう読むか(2)
頁末
前
次
目次
ユークリッド原論
第1巻
命題1ー16(外角と内対角)
外角・内対角
「なぜなら・・・であるから」
すべての三角形において
辺の一つが延長される
とき、
外角は
内対角のいずれよりも大きい。
-
三角形は定義1ー19の補足2による。
-
辺は定義1ー19の補足による。
-
外角とは、
三角形のある角について、
それをなす2辺のうち
一方の辺を延長したものと
他方の辺とがなす角のことである。
内対角とは、
三角形のある角について、
それ以外の2つの角のことである。
2つある内対角のうち、
一方は共通となる辺(直線)について同じ側にある
こととなり、
他方は共通となる辺について反対側にある
こととなる。
(以下、定義の補足(命題1ー16)という。)
ABCを三角形
とし、
その一辺BCがDまで延長された
とせよ。
外角ACDは
内対角CBA、BACのいずれよりも大きい
と主張する。
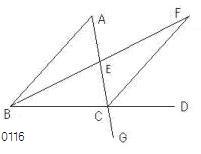
ACがEにおいて2等分され、
-
命題1ー10(作図・線分の2等分)
による。
-
E;中点(AC)
をとっている。
BEが結ばれ、
-
公準1ー1(作図.直線)
による。
-
線分(B,E)
をとっている。
一直線をなしてFまで延長され、
-
公準1ー2(作図.直線の延長)
による。
-
点F[延長BE]
をとっている。
EFがBEに等しくされ、
-
命題1ー3(作図・等しい線分を切り取る)
による。
論理的には、
一直線をなして十分延長しておいて、
命題1ー3
により
EFがBEに等しくなる
ように
Fをとる
ことになる。
-
EF=BE
となっている。
FCが結ばれ、
- 公準1ー1(作図.直線)
による。
-
線分(F,C)
をとっている。
ACがGまで延長された
とせよ。
【・・・(a)】
- 公準1ー2(作図.直線の延長)
による。
-
点G[延長AC]
をとっている。
そうすれば、
AEはECにBEはEFに等しい
から、
- (a)
による。
-
AE=EC、
BE=EF
となっている。
2辺AE、EBは
2辺CE、EFにそれぞれ等しい。
そして
角AEBは角FECに等しい。
なぜなら
対頂角である
から。
-
(a)
,
命題1ー15(対頂角)
による。
-
「なぜなら・・・であるから(for)」と
簡潔な論拠を後から示している。
以下、コメント2(命題1ー16)(なぜなら…であるから)という。
コメント(命題1ー4)を参照のこと。
-
(AE,EB)=(CE,EF)
∠AEB=∠FEC
となっている。
ゆえに
底辺ABは底辺FCに等しく、
三角形ABEは三角形CFEに等しく、
残りの2角は残りの2角に、
すなわち
等しい辺が対する角はそれぞれ等しい。
-
命題1ー4(2辺挟角相等)
による。
-
AB=FC、
△ABE≡△CFE
となっている。
したがって
角BAEは角ECFに等しい。
【・・・(1)】
ところが
角ECDは角ECFより大きい。
-
EはBDについてAと同じ側にあり、
Fも同じ側にある。
また、
FはACについてDと同じ側にある。
したがってFは角ACDの内部にある。
公理1ー8(大きい)
による。
-
∠ECD=∠ECF
となっている。
それゆえ
角ACDは角BAEより大きい。
同様にして
BCが2等分される
とき、
角BCGすなわち角ACDが
角ABCより大きい
ことも証明される。
よって
すべての三角形において
辺の一つが延長される
とき、
外角は内対角のいずれよりも大きい。
これが証明すべきことであった。
- 命題1-16は、
△ABC
において、
外角ACD>内対角CBA、BAC
のことである。
- 命題1-16は推論用命題である。
前
次
目次
頁頭
