ユークリッド原論をどう読むか(1)
頁末
前
次
目次
ユークリッド原論
第1巻
命題1ー2(作図・線分)
与えられた点において
与えられた線分に等しい
線分をつくる
こと。
与えられた点をA、
与えられた線分をBC
とせよ。
このとき
点Aにおいて
与えられた線分BCに等しい
線分をつくら
ねばならぬ。
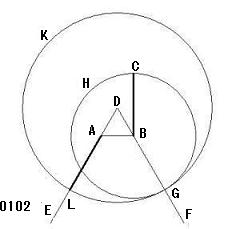
点Aから点Bへの線分ABが結ばれ、
-
公準1ー1(作図.直線)
による。
-
線分AB
をとる。
その上に
等辺三角形DABがつくられ、
【・・・(a)】
-
命題1ー1(作図・正三角形)
による。
-
点D[;;△DAB;等三[_AB])
となっている。
線分AE、BFが
DA、DBと一直線をなして延長され、
-
公準1ー2(作図.直線の延長)
による。
-
点E[延長DA]、
点F[延長DB]、
線分AE、線分BF
をとる。
中心B、半径BCをもって
円CGHが描かれ、
また、
中心D、半径DGをもって
円GKLが描かれた
とせよ。
【・・・(b)】
- 公準1ー3(作図.円)による。
-
点G;交点(DF、円(B、BC))、
点H;点[円(B、BC)]、
円CGH;円(B、BC)、
点L;交点(DE、円(D、DG))、
点K;点[円(D、DG)]
円GKL;円(D、DG)
となっている。
そうすれば、
点BはCGHの中心である
から、
BCはBGに等しい。
【・・・(1)】
また、
点Dは円GKLの中心である
から、
DLはDGに等しく、
-
前節、
定義1ー15(円)による。
-
BC=BG、
DL=DG
となっている。
そのうち、
DAはDBに等しい。
-
(a) 、
定義1ー20(等辺・二等辺・不等辺三角形)
による。
-
DA=DB
となっている。
それゆえ
残りのALは
残りのBGに等しい。
-
前節、前々節、
公理1ー3(等しいものから等しいものをひく)
による。
-
AL=BG
となっている。
ところが、
BGがBCに等しい
ことも先に証明された。
ゆえに
AL、BCの双方はBGに等しい。
-
前節、前々節による。
-
AL=BG、
BC=BG
となっている。
そして
同じものに等しいものは
また互いに等しい。
したがって
ALもBCに等しい。
-
前節、前々節による。
-
AL=BC、
となっている。
よって
与えられた点Aにおいて
与えられた線分BCに
等しい線分ALが
つくられている。
これが作図すべきものであった。
-
命題1ー2
により、
今日において通常考えられている円の作図
(任意の点と任意の半径による作図)
が可能である
こととなる。
なお、
命題1ー2の証明において、
点Cが唯一である必要がない
ことにも注目すべきである。
実際は
ABの上下に一点ずつある
が、仮に、
ABの上方に二点あったとしても
論証は成立している。
上方に一点しかないことの論証は
命題1ー7(3辺相等1)による。
-
原論の証明方法の特徴的なものに、
図形等を動かして重ねる
という方法がある。
この方法は命題1ー4(2辺挟角相等)に登場する
が、
この方法によれば、
この命題は次のように証明される。
点Bが点Aの上に置かれるように
線分BCを動かした
とき、
Cの位置をL
とする。
点Aと点Lを線分で結ぶ。
そうすれば、
線分ALと線分BCは
互いに重なり合うので等しい。
この命題は、
この方法によらず、
より論理的に証明しよう
という志向を示している。
なお、
線分については
この志向が成功している
が、
角になると
元来の動かして重ねるという方法によって
証明している。
この違いが、
原論の志向性と
当時の到達段階の状況を
示している
と見え、興味深い。
-
公理的志向のために、
命題1ー2を証明しようとし、
その前提となる命題1ー1(点)が
第一命題として位置づけられた
と見てよいだろう。
-
命題1-2は、
点A、
線分BC
に対して、
点D[;;△DAB;等三[_AB])
交点G(延長DB,円(B,BC))、
交点L(延長DA,円(D,DG))、
線分AL
をとると、
AL=BC
のことである。
-
命題1-2は作図用命題である。
前
次
目次
頁頭
