ユークリッド原論をどう読むか(10)
頁末
前
次
目次
ユークリッド原論
第6巻
命題6ー32(各2辺が比例し平行連結なら残辺が1直線)
もし
2辺が2辺に比例する
2つの三角形が
1つの角によって結ばれ、
それらの対応する辺が平行であるならば、
三角形の残りの辺は
1直線をなすであろう。
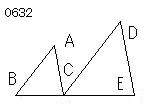
2つの三角形ABC、DCEが
2辺BA、ACが2辺DC、DEに比例し、
ABがACに対するように、
DCがDEに対し、
ABがDCに、
ACがDEに平行であるとせよ。
-
△ABCに対し、
命題1ー31(作図・平行線)
により
点D[平行線(C,BA)]
をとり、
命題1ー31(作図・平行線)
により
平行線DE"(D,AC)
をとり、
命題6ー12(作図.比例第4項)
により
線分D'E'[;;AB:AC=DC:D'E']
をとり、
命題1ー3の補足(作図.等しい線分となる点)
により
点E(DE";;DE=D'E')
をとる。
公準1ー1(作図.直線)
により
線分CE
をとり、
△DCEをつくる。
-
△ABC
に対し、
点D[平行線(C,BA)]、
点E(平行線(D,AC);;AB:AC=DC:DE)、
△DCE
をつくる。
BCは
CEと1直線をなす
と主張する。
ABは
DCに平行であり、
線分ACがそれらに会するから、
錯角BAC、ACDは互いに等しい。
【・・・(1)】
-
命題1ー29(平行と錯角、内対角、同側内角)
による。
-
∠BAC=∠ACD
となっている。
同じ理由で角CDEも角ACDに等しい。
それゆえ
角BACも角CDEに等しい。
【・・・(2)】
-
公理1ー1(同じものに等しい)
による。
-
∠BAC=∠CDE
となっている。
そして
ABC、DCEは
1つの角、
すなわち
角Aが
1つの角、
すなわち
角Dに等しく、
-
(2)による。
-
∠BAC=∠CDE
となっている。
等しい角をはさむ辺が比例し、
BAがACに対するように、
CDがDEに対する
2つの三角形であるから、
-
命題の設定による。
-
BA:AC=CD:DE
となっている。
三角形ABCは
三角形DCEに等角である。
-
命題6ー6(2辺が比例し挟角が等しい三角形は等角)
による。
-
△ABC(等角)△DCE
となっている。
ゆえに
角ABCは角DCEに等しい。
ところが
角ACDも角BACに等しい
ことが先に証明された。
-
(1)による。
-
∠ACD=∠BAC
となっている。
したがって
角ACE全体は
2角ABC、BACの和に等しい。
-
公理1ー2(等しいものに等しいものを加える)、
公理1ー7(等しい)
による。
-
∠ACE=∠ABC+∠BAC
となっている。
双方に
角ACBが加えられたとせよ。
そうすれば
角ACE、ACBの和は
角BAC、ACB、CBAの和に等しい。
-
公理1ー2(等しいものに等しいものを加える)
による。
-
∠ACE+∠ACB=∠BAC+∠ACB+∠CBA
となっている。
ところが
角BAC、ABC、ACBの和は
2直角に等しい。
-
命題1ー32(三角形の内対角・内角の和)
による。
-
∠BAC+∠ACB+∠CBA=2∠R
となっている。
それゆえ
角ACE、ACBの和も2直角に等しい。
-
公理1ー1(同じものに等しい)
による。
-
∠ACE+∠ACB=2∠R
となっている。
ゆえに
線分ACに対して
そのうえの点Cにおいて
同じ側にない2直線BC、CEが
接角ACE、ACBの和を
2直角に等しくする。
したがって
BCはCEと1直線をなす。
-
命題1ー14(直線と2直角2)
による。
-
点E;上.延長BC
となっている。
よってもし
2辺が2辺に比例する
2つの三角形が
1つの角によって結ばれ、
それらの対応する辺が平行であるならば、
三角形の残りの辺は
1直線をなすであろう。
これが証明すべきことであった。
- 命題6ー32は、
△ABC
に対し、
点D[平行線(C,BA)]、
点E(平行線(D,AC);;AB:AC=DC:DE)、
△DCE
をとれば、
E;上.延長BC
のことである。
- 命題6ー32は推論用命題である。
前
次
目次
頁頭
