ユークリッド原論をどう読むか（７）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第３巻

命題３ー２７（弧が等しければ角も等しい）
等しい円において
等しい弧の上に立つ角は、
　中心角も円周角も、
　互いに等しい。

• 等しいは、 公理１ー７ による。
• 円は、 定義１ー１５ による。
• 弧は、 定義１ー１８の補足 による。
• 角は、 定義１ー８ による。
• 中心角は、 定義の補足２（命題３ー２０） による。
• 円周角は、 定義の補足３（命題３ー２０） による。

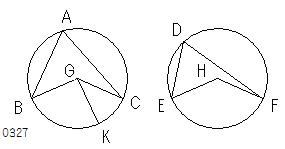
等しい円ＡＢＣ、ＤＥＦにおいて
　等しい弧ＢＣ、ＥＦ上に
　中心Ｇ、Ｈにおいて
　角ＢＧＣ、ＥＨＦが、
　円周において
　角ＢＡＣ、ＥＤＦが立つとせよ。

• 　円ＡＢＣ
  に対して、
  　点Ｂ[上.円周ＡＢＣ]、
  　点Ｃ[上.円周ＡＢＣ,外.Ｂ]、
  　点Ａ[上.円周ＡＢＣ,外.Ｂ,外.Ｃ]、
  　中心Ｇ.円ＡＢＣ、
  　点Ｈ[]、
  　円ＤＥＦ(Ｈ,ＧＢ)、
  　点Ｅ[上.円周ＤＥＦ]、
  　点Ｆ(上.円周ＤＥＦ,同向側(ＥＨ,ＢＧ,Ｃ);;弧ＥＦ≡弧ＢＣ)
  　点Ｄ[上.円周ＤＥＦ,同向側(ＥＦ,ＢＣ,Ａ)]
  　線分ＢＧ、ＧＣ、ＢＡ、ＡＣ、
  　線分ＥＨ、ＨＦ、ＥＤ、ＤＦ
  をとっている。

角ＢＧＣは
　角ＥＨＦに等しく、
角ＢＡＣは
　角ＥＤＦに等しい
　と主張する。

もし
　角ＢＧＣが
　角ＥＨＦに
　等しくないならば、

• 背理法の仮定を述べている。

それらの一方は
　大きい。

• 公理１ー７の補足 （線分・角は大か等か小）
  による。

角ＢＧＣが
　大きいとし、 【・・・(a)】

• 本来は、
  　場合分けが必要である。
  すなわち、
  ＢＧＣが
  　ＥＨＦより
  　大きい場合、
  　等しい場合、
  　小さい場合
  　の３つである。
  等しい場合は
  　背理法の仮定に反していて
  　論証の必要がない。
  小さい場合は、
  　小さい方を
  　改めて
  　円ＤＥＦ、中心Ｈに
  　記号を付け直して
  　論証を進めればよい
  　という意味である。
• 　∠ＢＧＣ＞∠ＥＨＦ
  となっている。

　線分ＢＧ上に
　その上の点Ｇにおいて
　角ＥＨＦに等しい
角ＢＧＫが
　つくられたとせよ。 【・・・(b)】

• 命題１ー２３ （作図・直線上に指定された角）
  による。
• 　点Ｋ(上.円周ＡＢＣ,同向側(ＢＧ,ＥＨ,Ｆ);;∠ＢＧＫ＝∠ＥＨＦ)
  をとっている。

ところが
等しい角は
　中心においてあるとき、
　等しい弧の上に立つ。

• 命題３ー２６ （角が等しければ弧は等しい）
  による。

それゆえ
　弧ＢＫも
　ＥＦに等しい。

• (b) による。
• 　弧ＢＫ≡弧ＥＦ
  となっている。

しかるに
ＥＦは
　ＢＣに等しい。

• 命題の設定 命題３ー２６ （角が等しければ弧は等しい）
  による。
• 　弧ＥＦ≡弧ＢＣ
  となっていた。

ゆえに
　ＢＫも
　ＢＣに等しい。 【・・・(1)】

• 公理１ー１ （同じものに等しい）
  による。
• 　弧ＢＫ≡弧ＢＣ
  となっている。

すなわち
　小さいものが
　大きいものに等しい。

• 背理法の仮定と、
  　 公理１ー８の補足 （小さい）
  により
  ＢＫは
  　ＢＣより小さい。
  一方、
  　(1) により
  ＢＫは
  　ＢＣに等しい。

これは不可能である。
したがって
角ＢＧＣは
　角ＥＨＦに不等でない。

• 背理法による。

それゆえ
　等しい。

• 　∠ＢＧＣ＝∠ＥＨＦ
  となっている。

そして
　Ａにおける角も
　Ｄにおける角に等しい。

• 命題３ー２０ （中心角は円周角の２倍）
  による。
• 　∠ＢＡＣ＝∠ＥＤＦ
  となっている。

よって
　等しい円において
等しい弧の上に立つ角は、
　中心角も円周角も、
　互いに等しい。

これが証明すべきことであった。
　

• 命題３ー２７は、
  　円ＡＢＣ
  に対して、
  　円ＤＥＦ[円ＡＢＣ]、
  　弧ＥＦ..円ＤＥＦ[弧ＢＣ.円ＡＢＣ]、
  をとれば、
  　中心角ＢＧＣ.円ＡＢＣ＝中心角ＥＨＦ.円ＤＥＦ、
  　円周角ＢＡＣ.円ＡＢＣ＝円周角ＥＤＦ.円ＤＥＦ
  のことである。
  
• 命題３ー２７は推論用命題である。

  前提	作図	推論
  定義
  公準
  公理		1-1 ,1-7補 ,1-8補
  命題	1-23	3-20 ,3-26
  その他

前 　　 次 　　 目次 　　頁頭