ユークリッド原論をどう読むか(5)
頁末
前
次
目次
ユークリッド原論
第2巻
命題2ー1(任意個分割との矩形)
(作図.矩形)
もし2線分があり、
その一方が
任意個の部分に分けられるならば、
2線分にかこまれた矩形は、
分けられていない線分と
分けられた部分の
おのおのとにかこまれた
矩形の和に等しい。
A、BCを2線分とし、
BCが
点D、Eにおいて
任意に分けられたとせよ。
A、BCにかこまれた矩形は
A、BDにかこまれた矩形と
矩形A、DEおよび矩形A、ECとの和に
等しいと主張する。
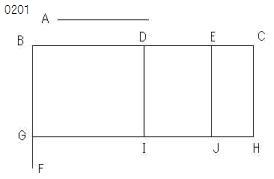
Bから
BCに直角にBFがひかれ、
BGが
Aに等しくされ、
- 命題1−3(作図・等しい線分を切り取る)による。
-
BG=Aとなっている。
Gを通り
BFに直角にGHがひかれ、
D、E、Cを通り
BGに平行にDI、EJ、CHがひかれたとせよ。
[・・・・・・(a)]
そうすれば
[矩形]BHは
BI、DJ、EHの和に等しい。
- 公理1−7(等しい)による。
-
rec(BH)
=rec(BI)+rec(DJ)+rec(EH)
[・・・・・・(1)]
(以下、rec( )は矩形を示す。)
そして
BHは
矩形A、BC[A、BCにかこまれた矩形]である。
なぜなら
GB、BCにかこまれ、
BGはAに等しいから。
-
「なぜなら・・・であるから」については、
コメント2(命題1ー16)(なぜなら…であるから)を参照のこと。
- 定義2ー1(かこまれる)による。
- BHは矩形A、BC「である」
として、
「等しい」ではないことに
注目すること。
これが定義に基づいた表現である。
-
rec(BH)=rec(A、BC)
[・・・・・・(2)]
また
BIは
矩形A、BDである。
なぜなら
GB、BDにかこまれ、
BGはAに等しいから。
-
「なぜなら・・・であるから」については、
コメント2(命題1ー16)(なぜなら…であるから)を参照のこと。
- 定義2ー1(かこまれる)による。
- rec(BI)=rec(A、BD)
[・・・・・・(3)]
そして
DJは
矩形A、DEである。
なぜなら
DI、すなわちBGは
Aに等しいから。
-
「なぜなら・・・であるから」については、
コメント2(命題1ー16)(なぜなら…であるから)を参照のこと。
- 定義2ー1による。
-
rec(DJ)=rec(A、DE)
[・・・・・・(4)]
同様にしてまた
EHは
矩形A、ECである。
- 定義2ー1(かこまれる)による。
-
rec(EH)=rec(A、EC)
[・・・・・・(5)]
それゆえ
矩形A、BCは
矩形A、BD、矩形A、DE、矩形A、ECの和に
等しい。
よってもし
2線分があり、
その一方が
任意個の部分に分けられるならば、
2線分にかこまれた矩形は、
分けられていない線分と
分けられた部分のおのおのとに
かこまれた矩形の和に等しい。
これが証明すべきことであった。
-
本命題の証明の先頭から
(a)までにより、
線分A、BCにかこまれた
矩形が作図できる。
(以下、命題2ー1の補足(作図.矩形)という。)
- 表現上は推論用命題であるが、
第2巻においては
命題を
既に証明された第2巻の命題をもとに
証明するという立場に立っていない。
すなわち、
この命題を根拠として
別の命題が証明されるという記述が、
命題2ー9に至ってようやく現れる。
- 命題2-1は、
A、BC;線分
に対して、
BC=BD、DE、EC
ならば、
rec(A、BC)
=rec(A、BD)+rec(A、DE)+rec(A、EC)
のことである。
-
命題2ー1の補足(作図.矩形)
- 命題2-1は推論用命題である。
前
次
目次
頁頭
