ユークリッド原論をどう読むか（１０）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第６巻

命題６ー１７（比例３線分と外項矩形、中項正方形）
(作図.線分上に矩形と等しい正方形)
(等しいものの比例中項は等しい)

もし
　３線分が比例する
　ならば、
　外項にかこまれた矩形は
　中項の上に立つ正方形に等しい。
そしてもし
　外項にかこまれた矩形が
　中項の上に立つ正方形に等しい
　ならば、
　３線分は
　比例するであろう。

• 線分は、 定義の補足（命題１ー１） による。
• 比例は、 定義５ー６ による。
• 外項は、 定義の補足（命題６ー１６） による。
• 矩形は、 定義１ー２２ による。
• 中項は、 定義の補足３（命題６ー８） による。
• 正方形は、 定義１ー２２ による。
• 等しいは、 公理１ー７ による。

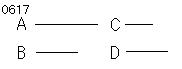
３線分Ａ、Ｂ、Ｃが比例する、
　すなわち
　ＡがＢに対するように、
　ＢがＣに対するとせよ。

• 命題６ー１３（作図.２線分の比例中項）
  による。
• 　Ａ、Ｂ
  に対して、
  　Ｃ[;;Ａ：Ｂ＝Ｂ：Ｃ]
  をとっている。

Ａ、Ｃにかこまれた矩形は
　Ｂ上の正方形に等しい
　と主張する。

《ＤがＢに等しいとせよ。》
［Ｂに等しい線分Ｄをひく。］ 【・・・(a)】

• 命題１ー２（作図・線分）
  による。
• 　Ｄ[;;Ｄ＝Ｂ]
  をとっている。

そうすれば
　ＡがＢに対するように、
　ＢがＣに対し、

• 命題の設定による。
• 　Ａ：Ｂ＝Ｂ：Ｃ
  となっている。

　ＢはＤに等しいから、

• (a)による。
• 　Ｂ＝Ｄ
  となっている。

　ＡがＢに対するように、
　ＤがＣに対する。

• 命題５ー７（同一量の比）、
  命題５ー１１（同一の比に同じ比）
  による。
• 　Ａ：Ｂ＝Ｄ：Ｃ
  となっている。

ところがもし
　４線分が比例するならば、
　外項にかこまれた矩形は
　内項にかこまれた矩形に等しい。

• 命題６ー１６（比例４線分と外項矩形、内項矩形）
  である。

それゆえ
　矩形Ａ、Ｃは
　矩形Ｂ、Ｄに等しい。

• 　矩形(Ａ,Ｃ)＝矩形(Ｂ,Ｄ)
  となっている。

ところが
　ＢはＤに等しいから、

• (a) による。
• 　Ｂ＝Ｄ
  となっている。

　矩形Ｂ、ＤはＢ上の正方形である。

• 定義１ー２２（正方形・矩形・菱形・長斜方形・トラペジオン）
  による。
• 　矩形(Ｂ,Ｄ)＝正方(_Ｂ)
  となっている。

ゆえに
　Ａ、Ｃにかこまれた矩形は
　Ｂ上の正方形に等しい。

• 公理１ー１（同じものに等しい）
  による。
• 　矩形(Ａ,Ｃ)＝正方(_Ｂ)
  となっている。

次に
　 矩形Ａ、Ｃが
　Ｂ上の正方形に等しいとせよ。

• 　矩形(Ａ,Ｃ)
  に対して、
  　命題６ー１３（作図.２線分の比例中項）
  により
  　Ｂ[;;Ａ：Ｂ＝Ｂ：Ｃ]、
  　正方(_Ｂ)
  をとれば、
  　本命題の前半により、
  　矩形(Ａ,Ｃ)＝正方(_Ｂ)
  となる。
  　この作図方法
  を前提とせず
  　仮想的に作図された
  として
  　後半を証明する。
• 　矩形(Ａ,Ｃ)＝正方(_Ｂ)
  をとっている。

ＡがＢに対するように、
　ＢがＣに対すると主張する。
　
同じ作図がなされたとき、 【・・・(b)】

• (a)のことである。
• 　Ｄ[;;Ｄ＝Ｂ]
  をとっている。

　矩形Ａ、ＣがＢ上の正方形に等しく、

• 命題の設定 による。
• 　矩形(Ａ,Ｃ)＝正方(_Ｂ)
  となっている。

　他方
　ＢはＤに等しいから、

• (a) による。
• 　Ｂ＝Ｄ
  となっている。

　Ｂ上の正方形は矩形Ｂ、Ｄである。

• 定義１ー２２（正方形・矩形・菱形・長斜方形・トラペジオン）
  による。
• 　正方(_Ｂ)＝矩形(Ｂ,Ｄ)
  となっている。

それゆえ
　矩形Ａ、Ｃは
　矩形Ｂ、Ｄに等しい。

• 公理１ー１（同じものに等しい）
  による。
• 　矩形(Ａ,Ｃ)＝矩形(Ｂ,Ｄ)
  となっている。

ところがもし
　外項にかこまれた矩形が
　内項にかこまれた矩形に等しければ、
　４線分は
　比例する。

• 命題６ー１６（比例４線分と外項矩形、内項矩形）
  による。

ゆえに
　ＡがＢに対するように、
　ＤがＣに対する。

• 　Ａ：Ｄ＝Ｂ：Ｃ
  となっている。

ところが
　ＢはＤに等しい。

• (b) による。
• 　Ｂ＝Ｄ
  となっている。

したがって
　ＡがＢに対するように、
　ＢがＣに対する。

• 命題５ー７（同一量の比）、
  命題５ー１１（同一の比に同じ比）
  による。
• 　Ａ：Ｂ＝Ｃ：Ｄ
  となっている。

よってもし
　３線分が比例するならば、
　外項にかこまれた矩形は
　中項の上に立つ正方形に等しい。
そしてもし
　外項にかこまれた矩形が
　中項の上に立つ正方形に等しいならば、
　３線分は
　比例するであろう。
これが証明すべきことであった。

• 　矩形ＣＤ、ＤＦと等しい
  　線分ＡＢ上の正方形をつくる
  ことができる。
  (以下、命題６ー１７の補足 (作図.線分上に矩形と等しい正方形)という。)
  なぜなら、
  　命題６ー１３（作図.２線分の比例中項）
  により、
  　ＣＤ：ＡＢ＝ＡＢ：ＤＦ
  となるＡＢをもとめ、
  　命題１−４６（作図.線分上に正方形） により
  　ＡＢ上に正方形をつくる
  ことができるから。
• 　命題６ー１７（比例３線分と外項矩形、中項正方形）
  　命題１−４８の補足（正方形の大等小と辺の大等小）
  により、
  　等しいものの比例中項は等しい。
  (以下、命題６ー１７の補足２ (等しいものの比例中項は等しい)という。)
  
• 命題６ー１７の補足 (作図.線分上に矩形と等しい正方形)

  前提	作図	推論
  定義
  公準
  公理
  命題	1-46,6-13
  その他

• 命題６ー１７の補足２ (等しいものの比例中項は等しい)

  前提	作図	推論
  定義
  公準
  公理
  命題		1-48補,6-17
  その他

• 命題６ー１７は推論用命題である。

  前提	作図	推論
  定義		1-22
  公準
  公理		1-1
  命題	1-2,6-13	5-7,5-11,6-16
  その他

前 　　 次 　　 目次 　　頁頭