ユークリッド原論をどう読むか(2)
頁末
前
次
目次
ユークリッド原論
第1巻
命題1ー11(作図・線分からの垂線)
(垂線は唯一)
与えられた直線に
その上の与えられた点から
直角に直線をひく
こと。
与えられた直線をAB、
その上の与えられた点をC
とせよ。
-
公準1ー1の補足(作図.任意の点をとる)
による。
-
直線(A,B)、
C;点[AB]
をとっている。
このとき
点Cから
直線ABに
直角に直線をひか
ねばならぬ。
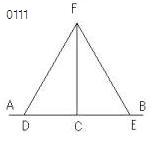
AC上に任意の点Dがとられ、
-
公準1ー1の補足(作図.任意の点をとる)
による。
-
D;点[CA]
をとっている。
CEがCDに等しくされ、
-
点Eが取れる
ことは、
命題1ー3(作図・等しい線分を切り取る)
による。
CBがCDより大きい
ことが前提されるが、
Bは直線の右側の任意の点である
から、
必要に応じてCBは
いくらでも大きくできる。
-
E;点(CB,CE=CD)
をとっている。
DE上に
等辺三角形FDEがつくられ、
-
命題1ー1(作図・正三角形)
による。
-
F;頂点.正三(_DE)
をとっている。
FCが結ばれた
とせよ。
【・・・(a)】
与えられた直線ABに
その上の与えられた点から
直角に直線FCがひかれている
と主張する。
線分(F,C)
をとっている。
DCはCEに等しく、
CFは共通である
から、
2辺DC、CFは
それぞれ
2辺EC、CFに等しい。
【・・・(1)】
-
まず、
二つの三角形の2辺が
それぞれ等しい
ことを確認している。
その後に、
挟角あるいは底辺が等しい
ことの確認にすすむ。
これが合同を証明する際のスタイルである。
-
(DC,CF)=(EC,CF)
となっている。
そして
底辺DFは底辺FEに等しい。
-
(a)により、
DFEは等辺三角形になる
ことによる。
-
DF=FE
となっている。
したがって、
角DCFは角ECFに等しい。
【・・・(2)】
-
(1),
命題1ー4(2辺挟角相等)
により、
二つの三角形は合同となる
ことによる。
-
∠DCF=∠ECF
となっている。
しかも
接角である。
ところが
直線が直線の上にたてられて
接角を互いに等しくする
とき、
等しい角の双方は直角である。
それゆえ
角DCF、FCEの双方は直角である。
よって
与えられた直線ABに
その上の与えられた点Cから
直角に直線CFがひかれている。
これが作図すべきものであった。
-
直線上の点から、
その直線に垂直な直線は唯一である。
(以下、命題1ー11の補足(垂線は唯一)という。)
もし
CFと異なる、
ABに垂直な直線CGがあった
とすると、
CGは
角ACFの内部か、
BCFの内部か
何れかをとおる。
ACFの内部をとおる
とすると、
CG上でACFの内部にある点を
公準1ー1の補足(作図.任意の点をとる)
によりとる。
この点を改めてG
とする。
角ACGは
ACFの内部にある
から
公理1ー8の補足(小さい)
により
ACFより小さい。
ところが
ACG、ACFは
直角で等しい
から、
これは不可能である。
背理法により、
直線上の点から、
その直線に垂直な直線は唯一である。
角BCFの内部をとおる
場合も
同様に証明できる。
- 命題1-11は、
AB;直線、
C;点[AB]
に対して、
D;点[AC]、
E;点(CB、CE=CD)、
F;頂点.等三(_DE)
をとるならば、
FC⊥AB
のことである。
-
命題1ー11の補足(垂線は唯一)
- 命題1-11は作図用命題である。
前
次
目次
頁頭
