ユークリッド原論をどう読むか（７）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第３巻

命題３ー３６（いわゆる方べきの定理２）
（いわゆる方べきの定理３）
もし
　円の外部に１点がとられ、
　それから円に
　２つの直線がひかれ、
それらの一方は
　円を切り、
他方は
　接する
　とすれば、
切る線分の全体と、
　外部に
　その点と凸型の弧との間に
　切り取られた線分とに
　　かこまれた矩形は
　接線の上の正方形に等しいであろう。

• 円は、 定義１ー１５ による。
• 点は、 定義１ー１ による。
• 直線は、 定義１ー４ による。
• 切るは、 定義３ー２の補足２ による。
• 接するは、 定義３ー２ による。
• 線分は、 定義の補足（命題１ー１） による。
• 凸型の弧は、 定義の補足３（命題３ー８） による。
• かこまれたは、 定義２ー１ による。
• 矩形は、 定義１ー２２ による。
• 接線は、 定義３ー２の補足３ による。
• 正方形は、 定義１ー２２ による。
• 等しいは、 公理１ー７ による。

円ＡＢＣの外部に
　任意の点Ｄがとられ、

• 公準１ー１の補足 による。

　Ｄから円ＡＢＣに
　２線分ＤＣＡ、ＤＢがひかれたとせよ。
そして
ＤＣＡは
　円ＡＢＣを切り、

• 円を切る直線の引き方は、
  　この後、
  　２つの場合に分けられる。

ＢＤは
　接するとせよ。

• 命題３ー１７ による。

ＡＤ、ＤＣにかこまれた矩形は
　ＤＢ上の正方形に等しい
　と主張する。

そこで
ＤＣＡは
　中心を通るか
　通らないか
　である。

• 場合分けである。

まず
　中心を通るとし、

• 第１の場合である。

　Ｆを
　円ＡＢＣの中心とし、 【・・・(a)】

• 命題３ー１ により、
  　中心をとり、
  　それをＦとする。
  公準１ー１ により
  　ＦとＤとを結ぶ。
  定義の補足３（命題３ー８） 、
  　 命題３ー８の補足４ により
  線分ＦＤは
  　円周と１つの交点をもち、
  　それをＣとする。
  公準１ー２ により
  　線分ＦＤをＦの方向に延長する。
  命題の補足３（定義１ー１４） により、
  　必要なだけ延長すれば
  延長した部分は
  　交点をもつ。
  定義の補足（命題３ー８） 、
  　 命題３ー８の補足２ により、
  交点は１つあり、
  　それをＡとする。
  Ａ、Ｃを溯って用いている。

　ＦＢが結ばれたとせよ。

• 命題３ー１７ により
  　Ｄから円ＡＢＣに
  　接線をひき、
  　接点をＢとする。
  Ｂを溯って用いている。
  公準１ー１ により
  　ＦとＢとを結ぶ。

そうすれば、
　角ＦＢＤは直角である。

• 命題３ー１８ による。

そして
弦ＡＣは
　Ｆにおいて２等分され、

• 定義１ー１７ により
  ＡＣは
  　直径であり、
  　 定義１ー１６ による。

　それに
　ＣＤが加えられたから、
矩形ＡＤ、ＤＣと
　ＦＣ上の正方形との和は
　ＦＤ上の正方形に等しい。 【・・・(1)】

• 命題２ー６ による。

ところが
ＦＣは
　ＦＢに等しい。

• (a) , 定義１ー１５ による。

ゆえに
矩形ＡＤ、ＤＣと
　ＦＢ上の正方形との和は
　ＦＤ上の正方形に等しい。

• (1) , 公理１ー２ 、 公理１ー１ による。

そして
ＦＢ、ＢＤ上の正方形の和は
　ＦＤ上の正方形に等しい。

• 命題１−４７ による。

したがって
矩形ＡＤ、ＤＣと
　ＦＢ上の正方形との和は
　ＦＢ、ＢＤ上の正方形の和に等しい。

• 公理１ー１ による。

双方から
　ＦＢ上の正方形がひかれたとせよ。
そうすれば
残りの矩形ＡＤ、ＤＣは
　接線のＤＢ上の正方形に等しい。

• 公理１ー３ による。
• 三平方の定理により
  　ＦＤ＾２＝ＦＢ＾２＋ＢＤ＾２
  　であるが、
  　ＦＤ＾２ーＦＢ＾２＝ＢＤ＾２
  　と変形して、
  　（ＦＤーＦＢ）（ＦＤ＋ＦＢ）＝ＢＤ＾２
  　と因数分解すると、
  　ＦＢ＝ＦＣ＝ＦＡであることに注意すれば、
  　（ＦＤーＦＣ）（ＦＤ＋ＦＡ）＝ＢＤ＾２
  　となり、
  　ＣＤ×ＡＤ＝ＢＤ＾２
  　となる。
  この式が求めるものであった。
  また、
  　ＦＤ＾２ーＦＣ＾２＝（ＦＤーＦＣ）（ＦＤ＋ＦＣ）
  　　　　　　　　　　＝ＣＤ×ＡＤ
  　この式こそが
  　命題２ー６である。
  逆に言えば、
  　円外の点から引いた
  　接線と
  　中心を通る線分と
  　　における上記の関係から
  　命題２ー６に注目することになったのではないか
  　とも考えられる。 　 　

次に
　ＤＣＡが
　円ＡＢＣの中心を通らないとし、

• 第２の場合である。

　中心Ｅがとられ、

• 命題３ー１ による。

　ＥからＡＣに
　垂線ＥＦがひかれ、 【・・・(b)】

• 公準１ー１の補足 により、
  　円内の中心Ｅ以外のところに
  　点Ｆをとり、
  　 公準１ー１ により
  　ＦとＤとを結ぶ。
  定義の補足３（命題３ー８） 、
  　 命題３ー８の補足４ により
  線分ＦＤは
  　円周と１つの交点をもち、
  　それをＣとする。
  公準１ー２ により
  　線分ＦＤをＦの方向に延長する。
  命題の補足３（定義１ー１４） により、
  　必要なだけ延長すれば
  延長した部分は
  　交点をもつ。
  定義の補足（命題３ー８） 、
  　 命題３ー８の補足２ により、
  交点は１つあり、
  　それをＡとする。
  Ａ、Ｃを溯って用いている。
  命題１ー１２ により、
  　ＥからＡＣに垂線をひく。
  命題３ー３ により
  　垂線は
  　弦ＡＣを２等分する。
  この点を改めてＦとする。
  　Ｆを溯って用いている。

　ＥＢ、ＥＣ、ＥＤが結ばれたとせよ。

• 公準１ー１ による。

そうすれば
　角ＥＢＤは直角である。

• (b) , 命題３ー１８ による。

そして
　中心を通る線分ＥＦが
　中心を通らない弦ＡＣを
　直角に切るから、
　それをまた２等分する。

• (b) , 命題３ー３ による。

それゆえ
ＡＦは
　ＦＣに等しい。
そして
弦ＡＣは
　点Ｆにおいて２等分され、
　それに
　ＣＤが加えられたから、
矩形ＡＤ、ＤＣと
　ＦＣ上の正方形との和は
　ＦＤ上の正方形に等しい。

• 命題２ー６ による。

双方に
　ＦＥ上の正方形が加えられたとせよ。
そうすれば
矩形ＡＤ、ＤＣと
　ＣＦ、ＦＥ上の正方形との和は
　ＦＤ、ＦＥ上の正方形の和に等しい。 【・・・(2)】

• 公理１ー２ による。

ところが
　角ＥＦＣは直角であるから、

• (b) による。

ＥＣ上の正方形は
　ＣＦ、ＦＥ上の正方形の和に等しい。

• 命題１−４７ による。
• これにより、
  　(2) の左辺、
  　すなわち、
  矩形ＡＤ、ＤＣと
  　ＣＦ、ＦＥ上の正方形との和は、
  　矩形ＡＤ、ＤＣとＥＣ上の正方形との和
  　に等しい。 【・・・(3)】

そして
ＥＤ上の正方形は
　ＤＦ、ＦＥ上の正方形の和に等しい。

• 命題１−４７ による。
• これにより、
  　(2) の右辺、
  　すなわち、
  ＦＤ、ＦＥ上の正方形の和は
  　ＥＤ上の正方形に等しい。

したがって
矩形ＡＤ、ＤＣと
　ＥＣ上の正方形との和は
　ＥＤ上の正方形に等しい。 【・・・(4)】

• (2),(3) 、 公理１ー１の補足 による。

ところが
ＥＣは
　ＥＢに等しい。

• (b), 定義１ー１５ による。

それゆえ
矩形ＡＤ、ＤＣと
　ＥＢ上の正方形との和は
　ＥＤ上の正方形に等しい。 【・・・(5)】

• (4), 公理１ー２ による。

また
角ＥＢＤは
　直角であるから、

• 命題３ー１８ による。

ＥＢ、ＢＤ上の正方形の和は
　ＥＤ上の正方形に等しい。

• 命題１−４７ による。

ゆえに
矩形ＡＤ、ＤＣと
　ＥＢ上の正方形との和は
　ＥＢ、ＢＤ上の正方形の和に等しい。

• (5), 公理１ー１ による。

双方から
　ＥＢ上の正方形がひかれたとせよ。
残りの矩形ＡＤ、ＤＣは
　ＤＢ上の正方形に等しい。

• 公理１ー３ による。

したがって、
　２つの場合の結果により
　矩形ＡＤ、ＤＣは
　接線のＤＢ上の正方形に等しい
よってもし
　円の外部に１点がとられ、
　それから円に
　２つの直線がひかれ、
それらの一方は
　円を切り、
他方は
　接するとすれば、
切る線分の全体と、
　外部に
　その点と凸型の弧との間に
　　切り取られた線分とにかこまれた矩形は
　接線の上の正方形に等しいであろう。
これが証明すべきことであった。

• 本命題により、
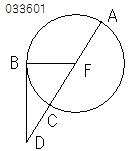
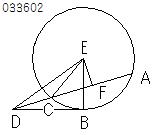
  「もし
  　円の外部に１点がとられ、
  　それから円に
  　２つの直線がひかれ、
  ともに
  　円を切るとすれば、
  それぞれの線分の全体と、
  　外部に
  　その点と凸型の弧との間に
  　切り取られた線分とに
  　　かこまれた矩形は
  　互いに等しい」
  　ことが証明される。
  （以下、「命題３ー３６の補足」（いわゆる方べきの定理３）という。）
  
  
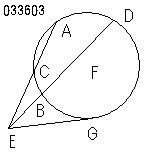
  　命題３ー１７（作図.円外の点から円への接線）
  により、
  円外の点から円に接線となる線分をひくと
  　命題３ー３６（いわゆる方べきの定理２）
  により、
  　円を切るそれぞれの線分の全体と、
  　外部に
  　その点と凸型の弧との間に
  　切り取られた線分とに
  　　かこまれた矩形は
  　ともに
  　接線の上の正方形に
  　等しくなるからである。
  
• 命題３ー３５とあわせて、いわゆる方べきの定理となる。
• 「命題３ー３６の補足」（いわゆる方べきの定理３）

  前提	作図	推論
  定義
  公準
  公理
  命題	3-17	3-36
  その他

• 命題３ー３６は推論用命題である。

  前提	作図	推論
  定義		1-15,1-16,1-17,補(題3-8),補3(題3-8)
  公準	1-1,1-1補,1-2
  公理		1-1,1-1補,1-2,1-3
  命題	補3(題1-14),1-12,3-1,3-8補2,3-8補4,3-17	1-47,2-6 ,3-3,3-18
  その他		場合分け

前 　　 次 　　 目次 　　頁頭