ユークリッド原論をどう読むか（７）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第３巻

命題３ー３５（いわゆる方べきの定理１）
もし
　円において
　２つの弦が
　互いに交わるならば、
一方の弦の
　２つの部分にかこまれた矩形は
　他方の弦の
　２つの部分にかこまれた矩形に
　等しい。

• 円は、 定義１ー１５ による。
• 弦は、 定義３ー４の補足 による。
• 交わるは、 定義１ー８の補足 による。
• かこまれたは、 定義２ー１ による。
• 矩形は、 定義１ー２２ による。
• 等しいは、 公理１ー７ による。

円ＡＢＣＤにおいて
　２つの弦ＡＣ、ＢＤが
　点Ｅにおいて
　互いに交わるとせよ。

• 　円ＡＢＣＤ
  に対して、
  　点Ａ[円周ＡＢＣＤ]、
  　点Ｃ[円周ＡＢＣＤ,外.Ａ]、
  　点Ｂ[内.弧ＡＣ]、
  　点Ｄ[円周ＡＢＣＤ,内.反対側(ＡＣ,Ｂ)]、
  　交点Ｅ(ＡＣ,ＢＤ)
  をとっている。

ＡＥ、ＥＣにかこまれた矩形は
　ＤＥ、ＥＢにかこまれた矩形に
　等しいと主張する。

［ 　ＡＣ、ＢＤが
　ともに中心を通る場合、
　ともに中心を通らない場合
　一方だけが中心を通る場合、
　がある。

ともに中心を通る場合、
］
そこでもし
　ＡＣ、ＢＤが中心を通り
　Ｅが
　円ＡＢＣＤの中心である
　ならば、

• ＡＣ、ＢＤが
  　中心を通るかどうかで
  　場合分けを行っているが、
  　後半の
  　　ＡＣ、ＢＤがともに中心を通らない場合の
  　　証明を見ると、
  　中心から垂線をひくことができるかどうか
  　　という観点から
  　場合分けを行っている
  　ことがわかる。
  とすれば、
  　ＡＣ、ＢＤが
  　ともに中心を通る場合、
  　ともに中心を通らない場合
  　一方だけが中心を通る場合、
  　の３つの場合に分けなければならない。
  原論の証明では、
  　第３の場合が抜けている。
  
• 場合分けの第１の場合である。
• 　Ｅ;中心.円ＡＢＣＤ
  となっている。

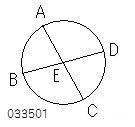
ＡＥ、ＥＣ、ＤＥ、ＥＢは
　等しいから

• 定義１ー１５ （円）
  による。
• 　ＡＥ＝ＥＣ＝ＤＥ＝ＥＢ
  となっている。

　ＡＥ、ＥＣにかこまれた矩形も
　ＤＥ、ＥＢにかこまれた矩形に
　等しいことは明らかである。

• 定義２ー１ （かこまれる）
  による。
• 　矩形(ＡＥ、ＥＣ)＝矩形(ＤＥ、ＥＢ)
  となっている。

［ ともに中心を通らない場合］

次に
　ＡＣ、ＤＢが中心を通らないとし、


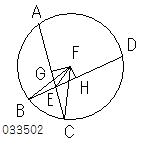
　円ＡＢＣＤの中心がとられ、
　それをＦとし、

• 場合分けの第２の場合である。
• 命題３ー１ （作図.円の中心）
  による。
• 　中心Ｆ.円ＡＢＣＤ
  をとっている。

　Ｆから
　弦ＡＣ、ＤＢに
　垂線ＦＧ、ＦＨがひかれ、 【・・・(a)】

• 命題１ー１２ （作図・線分への垂線）
  による。
  弦ＡＣと
  　ＦからＡＣにおろした垂線と
  　の交点をＧ、
  弦ＤＢと
  　ＦからＤＢにおろした垂線と
  　の交点をＨ
  　としている。
• 　垂線ＦＧ(Ｆ,ＡＣ)、
  　垂線ＦＨ(Ｆ,ＤＢ)
  をとっている。

　ＦＢ、ＦＣ、ＦＥが結ばれたとせよ。

• 公準１ー１ （作図.直線）
  による。
• 　線分ＦＢ、ＦＣ、ＦＥ
  をとっている。

そうすれば
　中心を通る線分ＧＦが
　中心を通らない弦ＡＣを
　直角に切るから、

• (a) による。
• 　ＧＦ;(通)中心.円ＡＢＣＤ
  　ＡＣ;¬(通)中心.円ＡＢＣＤ
  　ＧＦ⊥ＡＣ
  となっている。

　それをまた２等分する。

• 命題３ー３ （直径と弦）
  による。
• 　Ｇ;中点(ＡＣ)
  となっている。

それゆえ
　ＡＧはＧＣに等しい。

• 　ＡＧ＝ＧＣ
  となっている。

そこで
　弦ＡＣが
　Ｇにおいて等しい部分に、
　Ｅにおいて不等な部分に
　分けられたから、
ＡＥ、ＥＣにかこまれた矩形と
　ＥＧ上の正方形との和は
　ＧＣ上の正方形に等しい。

• 命題２ー５ （線分の矩形分割）
  による。
• 　ＥとＧが一致してても、
  　等式は成立する。
• 　矩形(ＡＥ,ＥＣ)＋正方(_ＥＧ)＝正方(_ＧＣ)
  となっている。

双方に
　ＧＦ上の正方形が加えられたとせよ。
そうすれば
矩形ＡＥ、ＥＣとＧＥ、ＧＦ上の正方形との和は
　ＣＧ、ＧＦ上の正方形の和に等しい。 【・・・(1)】

• 公理１ー２ （等しいものに等しいものを加える）
  による。
• 　矩形(ＡＥ,ＥＣ)＋正方(_ＥＧ)＋正方(_ＧＦ)
  　＝正方(_ＧＣ)＋正方(_ＧＦ)
  となっている。

ところが
ＦＥ上の正方形は
　ＥＧ、ＧＦ上の正方形の和に等しく、

• 命題１−４７ （三平方の定理）
  による。
• したがって、
  (1)により、
  矩形ＡＥ、ＥＣとＧＥ、ＧＦ上の正方形との和は
  　矩形ＡＥ、ＥＣとＦＥ上の正方形に等しくなる。
• 　正方(_ＦＥ)＝正方(_ＥＧ)＋正方(_ＧＦ)
  となり、
  　矩形(ＡＥ,ＥＣ)＋正方(_ＧＥ)＋正方(_ＧＦ)
  　＝矩形(ＡＥ,ＥＣ)＋正方(_ＦＥ)
  となっている。

ＦＣ上の正方形は
　ＣＧ、ＧＦ上の正方形の和に等しい。

• 命題１−４７ （三平方の定理）
  による。
• したがって、
  (1)により、
  矩形ＡＥ、ＥＣとＧＥ、ＧＦ上の正方形との和は
  　ＦＣ上の正方形に等しくなる。
• 　正方(_ＦＣ)＝正方(_ＣＧ)＋正方(_ＧＦ)
  となり、
  　矩形(ＡＥ,ＥＣ)＋正方(_ＧＥ)＋正方(_ＧＦ)
  　＝正方(_ＦＣ)
  となっている。

したがって
矩形ＡＥ、ＥＣとＦＥ上の正方形との和は
　ＦＣ上の正方形に等しい。

• 公理１ー１（同じものに等しい）
  による。
• 　矩形(ＡＥ,ＥＣ)＋正方(_ＥＦ)＝正方(_ＦＣ)
  となっている。

ところが
ＦＣは
　ＦＢに等しい。

• 定義１ー１５ （円）
  による。
• 　ＦＣ＝ＦＢ
  となっている。

それゆえ
矩形ＡＥ、ＥＣとＥＦ上の正方形との和は
　ＦＢ上の正方形に等しい。 【・・・(2)】

• 定義１ー２２ （正方形・矩形・菱形・長斜方形・トラペジオン） 、
  公理１ー１ （同じものに等しい）
  による。
• 　矩形(ＡＥ,ＥＣ)＋正方(_ＥＦ)＝正方(_ＦＢ)
  となっている。

同じ理由で
矩形ＤＥ、ＥＢとＦＥ上の正方形との和は
　ＦＢ上の正方形に等しい。
しかも
矩形ＡＥ、ＥＣとＦＥ上の正方形との和は
　ＦＢ上の正方形に等しいことも
　先に証明された。

• (2)による。
• 　矩形(ＤＥ,ＥＢ)＋正方(_ＥＦ)＝正方(_ＦＢ)、
  　矩形(ＡＥ,ＥＣ)＋正方(_ＥＦ)＝正方(_ＦＢ)
  となっている。

ゆえに
矩形ＡＥ、ＥＣとＦＥ上の正方形との和は
　矩形ＤＥ、ＥＢとＦＥ上の正方形との和
　に等しい。

• 公理１ー１ （同じものに等しい）
  による。
• 　矩形(ＤＥ,ＥＢ)＋正方(_ＥＦ)
  　＝矩形(ＡＥ,ＥＣ)＋正方(_ＥＦ)
  となっている。

双方から
　ＦＥ上の正方形がひかれたとせよ。
そうすれば
残りのＡＥ、ＥＣにかこまれた矩形は
　ＤＥ、ＥＢにかこまれた矩形
　に等しい。

• 公理１ー３ （等しいものから等しいものをひく）
  による。
• 　矩形(ＤＥ,ＥＢ)＝矩形(ＡＥ,ＥＣ)
  となっている。
• 　一方だけが中心を通る
  　第３の場合、
  　次のようになる。
  ＢＤだけが
  　中心を通っているとする。
  
  
  
  • 　ＢＤ;(通)中心.円ＡＢＣＤ
    となっている。
  
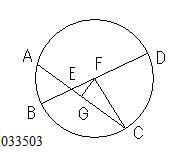
  命題３ー１ （作図.円の中心）
  により、
  円ＡＢＣＤの中心をとり、
  　それをＦとする。
  
  • 　中心Ｆ.円ＡＢＣＤ
    をとっている。
  
  命題１ー１２ （作図・線分への垂線）
  により、
  　Ｆから
  　弦ＡＣに
  　垂線をひき、
  　その交点をＧとする。
  
  • 　交点Ｇ(垂線(Ｆ,ＡＣ),ＡＣ)
    をとっている。
  
  公準１ー１ （作図.直線）
  により、
  　ＦＣ、ＦＥを結ぶ。
  
  • 　線分ＦＣ、ＦＥ
    をとっている。
  
  そうすれば
  　中心を通る線分ＧＦが
  　中心を通らない弦ＡＣを
  　直角に切るから、
  
  • 　ＧＦ;(通)中心Ｆ.円ＡＢＣＤ
    　ＡＣ;¬(通)中心Ｆ.円ＡＢＣＤ
    　ＧＦ⊥ＡＣ
    となっている。
  
  　 命題３ー３ （直径と弦）
  により、
  それをまた２等分する。
  
  • 　Ｇ;中点(ＡＣ)
    となっている。
  
  それゆえ
  　ＡＧはＧＣに等しい。
  
  • 　ＡＧ＝ＧＣ
    となっている。
  
  そこで
  　弦ＡＣが
  　Ｇにおいて等しい部分に、
  　Ｅにおいて不等な部分に
  　分けられたから、
  命題２ー５ （線分の矩形分割）
  により、
  　ＡＥ、ＥＣにかこまれた矩形と
  　ＥＧ上の正方形との和は
  　ＧＣ上の正方形に等しい。
  
  • 　矩形(ＡＥ,ＥＣ)＋正方(_ＥＧ)
    　＝正方(_ＧＣ)
    となっている。
  
  双方に
  　ＧＦ上の正方形を加えると、
  公理１ー２ （等しいものに等しいものを加える）
  により、
  　矩形ＡＥ、ＥＣとＧＥ、ＧＦ上の正方形との和は
  　ＣＧ、ＧＦ上の正方形の和に等しい。 【・・・(3)】
  
  • 　矩形(ＡＥ,ＥＣ)＋正方(_ＧＥ)＋正方(_ＧＦ)
    　＝正方(_ＣＧ)＋正方(_ＧＦ)
    となっている。
  ところが
  ＧＥ、ＧＦ上の正方形の和は
  　 命題１−４７ （三平方の定理）
  により、
  　ＦＥ上の正方形に等しく、
  
  • 　正方(_ＧＥ)＋正方(_ＧＦ)
    　＝正方(_ＦＥ)
    となっている。
  
  ＣＧ、ＧＦ上の正方形の和は
  　 命題１−４７ （三平方の定理）
  により、
  　ＦＣ上の正方形に等しい。
  • 　正方(_ＣＧ)＋正方(_ＧＦ)
    　＝正方(_ＦＣ)
    となっている。
  
  したがって
  (3)により、 矩形ＡＥ、ＥＣとＦＥ上の正方形との和は
  　ＦＣ上の正方形に等しい。
  
  • 　矩形(ＡＥ,ＥＣ)＋正方(_ＦＥ)＝正方(_ＦＣ)
    となっている。
  
  ところが
  定義１ー１５ （円）
  により、ＦＣは
  　ＦＢに等しい。
  
  • 　ＦＣ＝ＦＢ
    となっている。
  
  それゆえ
  定義１ー２２ （正方形・矩形・菱形・長斜方形・トラペジオン） 、
  公理１ー１ （同じものに等しい）
  により、
  矩形ＡＥ、ＥＣとＥＦ上の正方形との和は
  　ＦＢ上の正方形に等しい。
  • 　矩形(ＡＥ,ＥＣ)＋正方(_ＥＦ)＝正方(_ＦＢ)
    となっている。
  
  【・・・(4)】
  弦ＢＤは
  　中心Ｆにおいて等しい部分に、
  　Ｅにおいて不等な部分に
  　分けられているから、
  命題２ー５ （線分の矩形分割）
  により、
  ＢＥ、ＥＤにかこまれた矩形と
  　ＥＦ上の正方形との和は
  　ＦＢ上の正方形に等しい。
  
  • 　矩形(ＢＥ,ＥＤ)＋正方(_ＥＦ)＝正方(_ＦＢ)
    となっている。
  
  しかも
  矩形ＡＥ、ＥＣとＦＥ上の正方形との和は
  　ＦＢ上の正方形に等しいことも
  　先に証明された。
  
  • (4)による。
  • 　矩形(ＡＥ,ＥＣ)＋正方(_ＦＥ)
    　＝正方(_ＦＢ)
    となっている。
  ゆえに
  公理１ー１ （同じものに等しい）
  により、
  矩形ＡＥ、ＥＣとＦＥ上の正方形との和は
  　矩形ＤＥ、ＥＢとＦＥ上の正方形との和
  　に等しい。
  
  • 　矩形(ＡＥ,ＥＣ)＋正方(_ＦＥ)
    　＝矩形(ＤＥ,ＥＢ)＋正方(_ＦＥ)
    となっている。
  
  双方から
  　ＦＥ上の正方形がひかれたとせよ。
  そうすれば
  公理１ー３ （等しいものから等しいものをひく）
  により、
  残りのＡＥ、ＥＣにかこまれた矩形は
  　ＤＥ、ＥＢにかこまれた矩形
  　に等しい。
  
  • 　矩形(ＡＥ,ＥＣ)＝矩形(ＤＥ,ＥＢ)
    となっている。
  
  
• 第２の場合は、
  　上記の証明を前提とすれば、
  　弦ＡＣとＢＤとの交点Ｅと
  　中心Ｆと
  　　を通る直径ＧＨをひき、
  　矩形ＡＥ、ＥＣと
  　矩形ＢＥ、ＥＤと
  　がともに
  　矩形ＧＥ、ＥＨに等しい
  　ことから証明できる。
• 
  
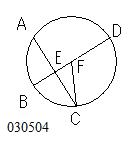
  第３の場合の特別な場合として、
  　ＢＤは中心を通り、
  　ＡＣは中心を通らず、
  　かつＡＣをＢＤが垂直２等分している
  　場合について、
  　命題の論証とは別に考える。
  　
  このとき、 三平方の定理により
  　ＦＣ＾２＝ＦＥ＾２＋ＥＣ＾２
  　であるが、
  　ＦＣ＾２ーＦＥ＾２＝ＥＣ＾２
  　と変形して、
  　（ＦＣーＦＥ）（ＦＣ＋ＦＥ）＝ＥＣ＾２
  　と因数分解すると、
  　ＦＣ＝ＦＢ＝ＦＤ、ＥＣ＝ＥＡであることに注意すれば、
  　（ＦＢーＦＥ）（ＦＤ＋ＦＥ）＝ＡＥ×ＥＣ
  　となり、
  　ＢＥ×ＥＤ＝ＡＥ×ＥＣ
  　となる。
  この式が求めるものであった。
  また、
  　ＦＤ＾２ーＦＥ＾２
  　＝（ＦＤーＦＥ）（ＦＤ＋ＦＥ）
  　＝（ＢＦーＦＥ）（ＦＤ＋ＦＥ）
  　＝ＢＥ×ＥＤ
  　この式こそが
  　命題２ー５（線分の矩形分割） である。
  逆に言えば、
  　円内の点から引いた
  　直径と
  　その直径に直交する弦と
  　　における上記の関係から
  　命題２ー５（線分の矩形分割） に注目することになったのではないか
  　とも考えられる。

［ したがって、
　３つの場合の結果により、
　ＡＥ、ＥＣにかこまれた矩形は
　ＤＥ、ＥＢにかこまれた矩形に
　等しい］

• 　矩形(ＡＥ,ＥＣ)＝矩形(ＤＥ,ＥＢ)
  となっている。

よってもし
　円において
　２つの弦が互いに交わるならば、
一方の弦の２つの部分にかこまれた矩形は
　他方の弦の２つの部分にかこまれた矩形
　に等しい。
これが証明すべきことであった。

• 命題３ー３５は、
  　円ＡＢＣＤ
  に対して、
  　弦ＡＣ..円ＡＢＣＤ、
  　弦ＢＤ..円ＡＢＣＤ、
  　交点Ｅ(ＡＣ,ＢＤ)
  をとれば、
  　矩形(ＡＥ,ＥＣ)＝矩形(ＢＥ,ＥＤ)
  のことである。
  
• 命題３ー３５は推論用命題である。

  前提	作図	推論
  定義		1-15,1-22,2-1
  公準	1-1
  公理		1-1,1-2,1-3
  命題	1-12,3-1	1-47,2-5 ,3-3
  その他		場合分け

前 　　 次 　　 目次 　　頁頭