ユークリッド原論をどう読むか（５）
頁末 　　 前 　　 次 　　 目次　

ユークリッド原論

第２巻

命題２ー６（線分の矩形外分割）
線分の矩形外分割
もし
　線分が２等分され、
　任意の線分が
　それと一直線をなして加えられるならば、
　加えられた線分を含んだ全体と
　加えられた線分とに
　かこまれた矩形と
　もとの線分の半分の上の正方形との和は、
　もとの線分の半分と
　加えられた線分と
　を合わせた線分上の正方形に等しい。

• 線分は、定義の補足（命題２ー１）による。
• 等分は、定義の補足２（公理１ー６）による。
• 直線は、定義１ー４による。
• かこまれたは、定義２ー１による。
• 矩形は、定義１ー２２による。
• 正方形は、定義１ー２２による。
• 半分は、定義の補足（公理１ー６）による。
• 等しいは、公理１ー７による。
• 　線分
  に対して、
  　線分の延長上に点をとり
  　その点と元の線分の両端とによる
  　２つの線分について、
  　一方の線分上に、
  　他の線分との矩形
  をとることを
  　線分の矩形外分割という。
  (以下、定義の補足(命題２ー６)(線分の矩形外分割)という。
  

線分ＡＢが
　点Ｃにおいて２等分され、
　線分ＢＤが
　それと一直線をなして
　加えられたとせよ。

• 　線分ＡＢ、
  　中点Ｃ(ＡＢ)、
  　点Ｄ[延長ＡＢ]
  をとっている。

ＡＤ、ＤＢにかこまれた矩形と
　ＣＢ上の正方形との和は
　ＣＤ上の正方形に等しいと主張する。
　


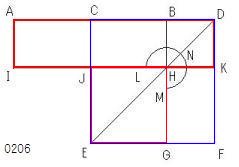
ＣＤ上に正方形ＣＥＦＤが描かれ、

• 命題１ー４６（作図.線分上に正方形）
  による。
• 　正方ＣＥＦＤ(_ＣＤ)
  をとっている。

ＤＥが結ばれ、

• 公準１ー１（作図.直線）
  による。
• 　線分ＤＥ
  をとっている。

また、
　Ｂを通り
　ＥＣ、ＤＦのどちらかに平行に
　ＢＧがひかれ、

• 命題１ー３１（作図・平行線）
  による。
  　命題１ー３０（平行の平行）
  により
  　どちらとも平行となる。
• 「どちらかに」については、
  　コメント（命題２ー２）を参照のこと
  
• 作図の設定により
  　辺ＥＦは辺ＣＤに平行で
  　ＢＧはＣＤと交わるから、
  　命題１ー３０の補足(交線に平行な線)
  により
  　ＥＦと交わる。
  　その交点を改めてＧとしている。
• 　交点Ｇ(ＥＦ,平行線(Ｂ,ＤＦ))
  をとっている。

点Ｈを通り、

• ＢＧは辺ＤＦと平行で、
  　ＤＥはＤＦと交わっているので、
  　命題１ー３０の補足(交線に平行な線)
  により
  　ＢＧとＤＥは交わり、
  　それをＨとする。
• 　交点Ｈ(ＤＥ,平行線(Ｂ,ＤＦ))
  をとっている。

ＡＢ、ＥＦのどちらかに平行に
　ＩＫがひかれ、

• 命題１ー３１（作図・平行線）
  による。
  　命題１ー３０（平行の平行）
  により
  　どちらとも平行となる。
• 辺ＡＤは辺ＤＦ、ＣＥと交わるから、
  　ＡＤに平行な直線は
  　命題１ー３０の補足(交線に平行な線)
  により
  　ＣＥ、ＤＦと交わり、
  　その交点を、それぞれＪ、Ｋとする。
• 　交点Ｊ(平行線(Ｈ,ＡＢ),ＣＥ)、
  　交点Ｋ(平行線(Ｈ,ＡＢ),ＤＦ)
  をとっている。

さらに
　Ａを通り
　ＣＪ、ＤＫのどちらかに平行に
　ＡＩがひかれたとする。

• 命題１ー３１（作図・平行線）
  による。
  　命題１ー３０（平行の平行）
  により
  　どちらとも平行となる。
• 直線ＪＫはＣＥと交わるから、
  　Ａを通りＣＥに平行な直線は
  　命題１ー３０の補足(交線に平行な線)
  により交わる。
  　その交点をＩとする。
• 　交点Ｉ(平行線(Ａ,ＣＪ),ＪＫ)
  をとっている。

そうすれば
　ＡＣはＣＢに等しいから、
　［矩形］ＡＪもＣＨに等しい。

• 定義２ー１（かこまれる）
  による。
• 　矩形(ＡＪ)＝矩形(ＣＨ)
  　　　　　　【・・・(1)】

ところが
　［矩形］ＣＨはＨＦに等しい。

• 命題１ー４３（平行四辺形の補形）
  による。
• 矩形(ＣＨ)＝矩形(ＨＦ)
  　　　　　　【・・・(2)】

それゆえＡＪもＨＦに等しい。

• 公理１ー１（同じものに等しい）
  による。
• (1) (2) より
  　矩形(ＡＪ)＝矩形(ＨＦ)
  　　　　　　【・・・(3)】

双方に
　ＣＫが加えられたとせよ。
そうすれば
　ＡＫ全体はグノーモーンＬＮＭに等しい。

• 公理１ー２（等しいものに等しいものを加える）、
  　公理１ー１の補足（等しいものに等しい）
  による。
• (3) より
  　矩形(ＡＪ)＋矩形(ＣＫ)＝矩形(ＨＫ)＋矩形(ＣＫ)
  となり、
  　矩形(ＡＫ)＝グ(ＬＮＭ)
  　　　　　　【・・・(4)】

ところが
　ＤＫはＤＢに等しいから、

• 命題２ー４の補足(正方形の対角線をはさむ正方形)
  により、
  　ＢＨＫＤは正方形となり、
  　定義１−２２（正方形・矩形・菱形・長斜方形・トラペジオン）
  により
  　ＤＫとＤＢは等しくなる。
• 　ＤＫ＝ＤＢ

ＡＫは
　矩形ＡＤ、ＤＢである。

• 定義２ー１（かこまれる）
  による。
• 　矩形(ＡＫ)＝矩形(ＡＤ、ＤＢ)
  　　　　　　【・・・(5)】

したがって
　グノーモーンＬＮＭも
　矩形ＡＤ、ＤＢに等しい。

• 公理１ー１の補足（等しいものに等しい）
  による。
• (4) (5) より
  　グ(ＬＮＭ)＝矩形(ＡＤ、ＤＢ)
  　　　　　　【・・・(6)】

双方に
　ＢＣ上の正方形に等しいＪＧが
　加えられたとせよ。

• 　矩形(ＪＧ)＝正方(_ＢＣ)
  　　　　　　【・・・(7)】

そうすれば
　ＡＤ、ＤＢにかこまれた矩形と
　ＣＢ上の正方形との和は
　グノーモーンＬＮＭとＪＧとの和に等しい。

• 公理１ー２（等しいものに等しいものを加える）
  による。
• (6) (7) より
  　矩形(ＡＤ、ＤＢ)＋正方(_ＣＢ)
  　＝グ(ＬＮＭ)＋矩形(ＪＧ)
  　　　　　　【・・・(8)】

ところが、
　グノーモーンＬＮＭとＪＧとの和は
　ＣＤ上の正方形全体である。

• 公理１ー７（等しい）
  による。
• 　グ(ＬＮＭ)＋矩形(ＪＧ)＝正方(_ＣＤ)
  　　　　　　【・・・(9)】

ゆえに
　ＡＤ、ＤＢにかこまれた矩形と
　ＣＢ上の正方形との和は
　ＣＤ上の正方形に等しい。
　

• 公理１ー１（同じものに等しい）
  による。
• (8) (9) より
  　矩形(ＡＤ、ＤＢ)＋正方(_ＢＣ)＝正方(_ＣＤ)

よってもし
　線分が２等分され、
　任意の線分が
　それと一直線をなして加えられるならば、
　加えられた線分を含んだ全体と
　加えられた線分とに
　かこまれた矩形と
　もとの線分の半分の上の正方形との和は、
　もとの線分の半分と
　加えられた線分とを合わせた
　線分上の正方形に等しい。
　
これが証明すべきことであった。

• 第２巻の命題のより、
  　以下の証明が可能である。
  矩形ＡＤ、ＤＢは、
  　命題２ー１（任意個分割との矩形）
  により、
  　矩形ＡＣ、ＤＢとＣＤ、ＤＢと
  　ＢＤ、ＤＢとの和に等しい。
  
  • 　矩形(ＡＤ、ＤＢ)
    　＝矩形(ＡＣ、ＤＢ)＋矩形(ＣＤ、ＤＢ)
    　＋矩形(ＢＤ、ＤＢ)
    　　　　　　【・・・(10)】
  作図の設定により
  　辺ＡＣはＣＢに等しいから、
  　矩形ＡＣ、ＤＢは
  　定義２ー１（かこまれる）
  により
  　ＣＤ、ＤＢである。
  
  • 　矩形(ＡＣ、ＤＢ)＝矩形(ＣＤ、ＤＢ)
    　　　　　　　【・・・(11)】
  また、
  　矩形ＢＤ、ＤＢは
  　定義２ー１（かこまれる）
  により
  　ＤＢ上の正方形である。
  
  • 　矩形(ＢＤ、ＤＢ)＝正方(_ＤＢ)
    　　　　　　　【・・・(12)】
  よって、
  　公理１ー１（同じものに等しい）、
  　公理１ー２（等しいものに等しいものを加える）
  により、
  　矩形ＡＤ、ＤＢは、
  　矩形ＣＤ、ＤＢの２倍と
  　ＤＢ上の正方形との和に等しい。
  
  • (10) (11) (12) により　
    　矩形(ＡＤ、ＤＢ) 　＝２×矩形(ＣＤ、ＤＢ)＋正方(_ＤＢ)
    　　　　　　【・・・(13)】
  双方に、
  　ＣＢ上の正方形を加えると、
  　公理１ー２（等しいものに等しいものを加える）
  により、
  　矩形ＡＤ、ＤＢとＣＢ上の正方形との和は、
  　矩形ＣＤ、ＤＢの２倍と
  　ＤＢ上の正方形とＣＢ上の正方形との和に等しい。
  
  • (13) により
    　矩形(ＡＤ、ＤＢ)＋正方(_ＣＢ)
    　＝２×矩形(ＣＤ、ＤＢ)＋正方(_ＤＢ)
    　＋正方(_ＣＢ)
    　　　　　　【・・・(14)】
  矩形ＣＤ、ＤＢの２倍と
  　ＤＢ上の正方形とＣＢ上の正方形との和は、
  　命題２ー４（２分線分上の正方形）
  により
  　ＣＤ上の正方形に等しい。
  
  • 　２×矩形(ＣＤ、ＤＢ)＋正方(_ＤＢ)
    　＋正方(_ＣＢ)
    　＝正方(_ＣＤ)
    　【・・・(15)】
  よって、
  　公理１ー１（同じものに等しい）
  により、
  　矩形ＡＤ、ＤＢとＣＢ上の正方形との和は、
  　ＣＤ上の正方形に等しい。
  
  • (14)< b>(15) から
    　矩形(ＡＤ、ＤＢ)＋正方(_ＣＢ)
    　＝正方(_ＣＤ）
    
• 本質的には、和と差の積は平方の差のことである。
  Ｘ＝（ＡＢ／２）＋ＢＤ、ｄ＝ＡＢ／２とおくと、
  （Ｘ＋Ｙ）（ＸーＹ）＝Ｘ^2ーＹ^2
  
• 　差ＡＤーＢＤと積ＡＤ×ＢＤの値
  を既知として、
  　ＡＤとＢＤ
  を求める方法、
  つまり、
  　今日的にいう２次方程式の解の公式
  を図形的に示している。
  すなわち、
  　Ｚ；正方(_Ｚ)＝正方(_差／２)＋積
  をとると、
  　ＡＤ＝差／２＋Ｚ、
  　ＢＤ＝差／２ーＺ
  として求められる。
  
• 命題2-6は、
  　ＡＢ；線分、
  に対して、
  　Ｃ；中点（ＡＢ）、
  　Ｄ；点[延長ＡＢ]
  をとるならば、
  　矩形(ＡＤ、ＤＢ)＋正方(_ＣＢ)＝正方(_ＣＤ)
  ことである。
• 命題2-6は推論用命題である。
  

  前提	作図	推論
  定義		2-1
  公準	1-1
  公理		1-1,1-2
  命題	1-30補,1-31,1-46	1-30,1-43,2-4補
  その他		どちらかに

  　
  
• 命題2-6は第２巻の命題によると次のようになる。
  

  前提	作図	推論
  定義		2-1
  公準
  公理		1-1,1-2
  命題		2-1,2-4
  その他

前 　　 次 　　 目次 　　頁頭