ユークリッド原論をどう読むか（２）
頁末 　　 前 　　 次 　　 目次　

ユークリッド原論
第１巻

命題１ー１２（作図・線分への垂線）　
（垂線は唯一）
（直線と円との交点は２つ以下）

　与えられた無限直線に
　その上にない与えられた点から
　垂線を下ろす
こと。

• 　命題１ー11は
  　直線上の点から垂線を延ばし、
  　命題１ー12は
  　直線上にない点から垂線を下ろす。
• 　直線は定義１ー４による。
• 　点は定義１ー１による。
• 　垂線は定義１ー１０による。

　与えられた無限直線をＡＢ
とし、
　その上にない与えられた点をＣ
とせよ。

• 　直線ＡＢ、
  　点Ｃ[ＡＢ外]
  をとっている。

このとき
　与えられた無限直線ＡＢに
　その上にない与えられた点Ｃから
　垂線を下ろさ
ねばならぬ。
　

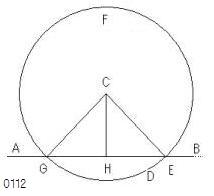
　直線ＡＢの反対側に
　任意の点Ｄがとられ、

• 　反対側
  は、
  　定義１ー７の補足（同じ側・反対側(平面)）
  による。
  　「直線ＡＢについてＣと反対側」
  という意味である。
• 　公準１ー１の補足（作図.任意の点をとる）
  による。
• 　点Ｄ[ＡＢ外、Ｃの反対側]
  をとっている。

　中心Ｃ半径ＣＤをもって
　円ＥＦＧが描かれ、

• 　公準１ー３（作図.円）
  による。
• 　円と直線との交点が
  　２つ存在するかどうか
  が論証の要点であるが、
  　原論では論証されていない。
  　これは、次のように論証できる。
  　
  もし
  　直線ＣＤが直線ＡＢと交わらない
  とすれば、
  　定義１ー23（平行(線)）
  により
  　平行になる
  から、
  　直線ＣＤ上のどの点も
  　直線ＡＢについて同じ側になる。
  
  　これは、
  　ＤがＣと反対側にあるということに矛盾する。
  
  　背理法により
  　直線ＣＤは直線ＡＢと交わる。
  
  　交点をＩとする。
  
  そこで
  　公準１ー3（作図.円）
  により
  　中心Ｃ半径ＣＤをもって円を描く。
  
  そうすると、
  　ＣとＤは
  　直線ＡＢについて反対側にある
  から、
  　線分ＣＤ上に（端ではなく）Ｉがある。
  
  　ＣＩは半径より小さい
  ので
  　円の内部にある。
  また、
  　直線ＡＢは無限直線である
  から、
  　ＡとＢとが円の外部にある
  としてもよい。
  したがって
  　命題の補足３（定義１ー１４）（図形と直線の交点）
  により、
  　線分ＡＩ上、ＢＩ上にそれぞれ交点がある。
  なお、
  　この命題の証明においては
  　それぞれの交点が唯一であることまでは
  　要求されない。
  
  　それぞれの一つをＧ、Ｅとすればよい。
• 　円ＥＦＧ(Ｃ,ＣＤ)、
  　Ｅ、Ｇ;交点(ＡＢ,円ＥＦＧ)
  をとっている。

　線分ＥＧがＨにおいて２等分され、

• 　命題１ー10（作図・線分の２等分）
  による。
• 　Ｈ;中点(ＥＧ)
  をとっている。

　線分ＣＧ、ＣＨ、ＣＥが結ばれた
とせよ。
　　　　　　【・・・(a)】

• 　公準１ー1（作図.直線）
  による。
• 　線分ＣＧ、ＣＨ、ＣＥ
  をとっている。

［そうすれば］
　与えられた無限直線ＡＢに
　その上にない与えられた垂線点Ｃから
　垂線ＣＨがひかれている
と主張する。

　ＧＨはＨＥに等しく、

• 　(a) による。
• 　ＧＨ＝ＨＥ
  となっている。

　ＨＣは共通である
から、
　２辺ＧＨ、ＨＣは
　２辺ＥＨ、ＨＣにそれぞれ等しい。
そして、
　底辺ＣＧは底辺ＣＥに等しい。

• 　前節、 　(a)、
  　定義１ー15（円）
  による。
• 　(ＧＨ,ＨＣ)＝(ＥＨ,ＨＣ)、
  　ＣＧ＝ＣＥ
  となっている。

したがって
　角ＣＨＧは角ＥＨＣに等しい。

• 　前節、
  　命題１ー8（３辺相等２）
  により、
  　三角形ＧＨＣとＥＨＣが、
  　合同となっているから。
• 　∠ＣＨＧ＝∠ＥＨＣ
  となっている。

　そして接角である。

• 　∠ＣＨＧ、∠ＥＨＣ;接角
  となっている。

ところが
　直線が直線の上に立てられて
　接角を互いに等しくする
とき、
　等しい角の双方は直角であり、
　立てられた直線は
　その下の直線に対して垂線
とよばれる。

• 　定義１ー10（直角）
  のことである。
  これにより、
  　ＣＨは垂線となっている。　

よって
　与えられた無限直線ＡＢに
　その上にない与えられた点Ｃから
　垂線ＣＨが下ろされている。

• 　ＣＨ⊥ＡＢ
  となっている。

　
　これが作図すべきものであった。

• 直線外の点から
  　その直線へ下ろした垂線は唯一である。
  　（以下、命題１ー１２の補足（垂線は唯一）という。）
  　背理法の仮定として、
  　直線ＡＢ外の点Ｃから
  　ＡＢへの垂線が２本ある
  とする。
  そうすれば、
  　それぞれ、
  　異なる点Ｈ、ＬでＡＢと交わる。
  なぜならば、
  　同一の点で交われ
  ば、
  　公理１ー９（２点を通る直線は一致）
  により、
  　同一の直線となる
  からである。
  そうすると、
  　同側内角の和は、
  　どちらも直角である
  から、
  　２直角となり、
  　ＣＨとＣＬ
  は公準１ー５（平行線公準）
  により平行となる
  が、
  　交点Ｃがある
  ので
  　矛盾する。
  よって
  　背理法により、垂線は唯一である。
  　命題１ー１６（外角と内対角）
  が証明された後であれ
  ば、
  　公準１ー５（平行線公準）
  を前提としない。
• 　直線と円との交点は２つ以下である。
  （以下、命題１ー１２の補足２（直線と円との交点は２つ以下）という。）
  　背理法の仮定として、
  　直線ＡＢと円ＥＦＧの交点が
  　Ｇ、Ｅ以外にＫがあった
  とする。
  　線分ＥＫを2等分する点をＬ
  とすると、
  　ＣＬも直線ＡＢの垂線となる。
  したがって、
  　直線ＡＢと交わる２直線ＣＨ、ＣＬがある
  ことになる。
  　これ
  は、命題１ー１２の補足（垂線は唯一）
  に矛盾する。
  よって
  　Ｇ、Ｅ以外には交点がない
  ことがわかる。
  
• なお、
  　この命題の証明では
  　あくまで公準１ー５（平行線公準）
  は
  　要求されていない。
• 　命題1-12は、
  　ＡＢ；直線、
  　Ｃ；点[ＡＢ外]
  に対して、
  　Ｄ；点[ＡＢ外,Ｃと反対側]、
  　Ｅ、Ｇ；交点(ＡＢ,円(Ｃ,ＣＤ))、
  　Ｈ；中点(ＥＧ)
  をとるならば、
  　ＣＨ⊥ＡＢ
  のことである。
  
• 命題１ー１２の補足２（直線と円との交点は２つ以下）

  前提	作図	推論
  定義
  公準
  公理
  命題		1-12補
  その他

• 命題１ー１２の補足（垂線は唯一）

  前提	作図	推論
  定義
  公準	1-5
  公理		1-9
  命題
  その他

• 　命題1-12は作図用命題である。

  前提	作図	推論
  定義		1-7補、1-10、1-15、1-23
  公準	1-1、1-1補、1-3
  公理
  命題	補3(義1-14),1-10	1-8
  その他

前 　　 次 　　 目次 　　頁頭