ユークリッド原論をどう読むか（４）
頁末 　　 前 　　 次 　　 目次　

ユークリッド原論
第１巻

命題１−４７（三平方の定理）
直角三角形において
　直角の対辺の上の正方形は
　直角をはさむ２辺の上の
　正方形の和に等しい。

• 直角三角形は、定義１−２１による。
• 直角は、定義１−１０による。
• 対辺は、定義１−２２の補足による。
• 正方形は、定義１−２２による。
• 辺は、定義１−１９の補足による。

ＡＢＣを
　角ＢＡＣを直角とする
　直角三角形とせよ。

• 　線分ＡＢ
  　線分ＡＣ[;;∠ＢＡＣ＝∠Ｒ]
  　△ＡＢＣ
  をとっている。

ＢＣ上の正方形は
　ＢＡ、ＡＣ上の正方形の和に等しい
　と主張する。


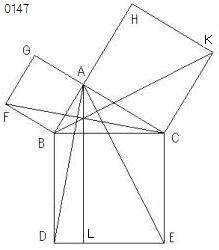
ＢＣ上に正方形ＢＤＥＣが、
　ＢＡ、ＡＣ上に正方形ＧＢ、ＨＣが
　描かれ、 【・・・(a)】

• 命題１−４６（作図.線分上に正方形）
  による。
• 　正方ＢＤＥＣ(_ＣＢ,反対側(ＣＢ,Ａ))
  　正方ＡＧＦＢ(_ＢＡ,反対側(ＢＡ,Ｃ))
  　正方ＣＫＨＡ(_ＡＣ,反対側(ＡＣ,Ｂ))
  をとっている。

Ａを通り
　ＢＤ、ＣＥのどちらかに平行に
　ＡＬがひかれたとせよ。 【・・・(b)】

• 命題１−３１（作図・平行線）
  による。
• 　交点Ｌ(ＤＥ,平行線(Ａ,ＢＤ))
  　線分ＡＬ
  をとっている。

そして
　ＡＤ、ＦＣが結ばれたとせよ。

• 公準１−１（作図.直線）
  による。
• 　線分ＡＤ、線分ＦＣ
  をとっている。

そうすれば
　角ＢＡＣ、ＢＡＧの双方は
　直角であるから、

• (a) による。
• 　∠ＢＡＣ＝∠ＢＡＧ＝∠Ｒ
  となっている。

　任意の線分ＢＡに対して
　その上の点Ａにおいて
　同じ側にない
　２線分ＡＣ、ＡＧが
　接角を２直角に等しくする。
それゆえ
　ＣＡはＡＧと一直線をなす。

• 命題１−１４（直線と２直角２）
  による。
• 　ＣＡ;ＡＧと一直線
  となっている。

同じ理由で
　ＢＡもＡＨと一直線をなす。

• 　ＢＡ;ＡＨと一直線
  となっている。

そして
　角ＤＢＣは
　角ＦＢＡに、
　ともに直角であるがゆえに
　等しいから、

• (a) による。
• 　∠ＤＢＣ＝∠ＦＢＡ
  となっている。

　双方に
　角ＡＢＣが加えられたとせよ。
そうすれば
　角ＤＢＡ全体は角ＦＢＣ全体に等しい。 【・・・(1)】

• 公理１−２（等しいものに等しいものを加える）
  による。
• 　∠ＤＢＡ＝∠ＦＢＣ
  となっている。

そして
　ＤＢはＢＣに等しく、
　ＦＢはＢＡに等しいから、
　２辺ＤＢ、ＢＡは
　２辺ＦＢ、ＢＣにそれぞれ等しい。
そして
　角ＤＢＡは角ＦＢＣに等しい。
したがって
　底辺ＡＤは底辺ＦＣに等しく、
　三角形ＡＢＤは三角形ＦＢＣに等しい。

• (a) (1) 命題１−４（２辺挟角相等）
  による。
• 　△ＡＢＤ＝△ＦＢＣ
  となっている。

そして
　平行四辺形ＢＬは
　三角形ＡＢＤの２倍である。
なぜなら
　それらは
　同じ底辺ＢＤをもち
　かつ
　同じ平行線ＢＤ、ＡＬの間にある
　から≪、≫［。］

• (b) ,命題１−４１（同一底辺上の平行四辺形と三角形の面積）
  による。
• 「なぜなら・・・であるから」については、
  　コメント２（命題１ー１６）を参照のこと。
• 　平四ＢＬ＝２×△ＡＢＤ
  となっている。

そして
　正方形ＧＢは
　三角形ＦＢＣの２倍である。
なぜなら
　これらもまた
　同じ底辺ＦＢをもち
　かつ
　同じ平行線ＦＢ、ＧＣの間にある
から。

• (a) ,命題１−４１（同一底辺上の平行四辺形と三角形の面積）
  による。
• 「なぜなら・・・であるから」については、
  　コメント２（命題１ー１６）を参照のこと。
• 　正方ＧＢ＝２×△ＦＢＣ
  となっている。

それゆえ
　平行四辺形ＢＬは
　正方形ＦＢに等しい。

• 公理１−１（同じものに等しい）
  による。
• 　平四ＢＬ＝正方(_ＦＢ)
  となっている。

同様にして
　ＡＥ、ＢＫが結ばれれば、
　平行四辺形ＣＬが
　正方形ＨＣに等しい
　ことも証明されうる。
ゆえに
　正方形ＢＤＥＣ全体は
　二つの正方形ＧＢ、ＨＣの和に等しい。

• 公理１−２（等しいものに等しいものを加える）
  による。
• 　正方ＢＤＥＣ＝正方ＧＢ＋正方ＨＣ
  となっている。

そして
　正方形ＢＤＥＣは
　ＢＣ上に描かれ、
　ＧＢ、ＨＣは
　ＢＡ、ＡＣ上に描かれている。

• 　正方ＢＤＥＣ;正方(_ＢＣ)
  　正方ＧＢ;正方(_ＢＡ)
  　正方ＨＣ;正方(_ＡＣ)
  となっている。

したがって
　辺ＢＣ上の正方形は
　辺ＢＡ、ＡＣ上の正方形の和に等しい。

• 　前節、前々節による。
• 　正方(_ＢＣ)＝正方(_ＢＡ)＋正方(_ＡＣ)
  となっている。

よって
　直角三角形において
　直角の対辺の上の正方形は
　直角をはさむ２辺の上の正方形の和に等しい。
　
これが証明すべきことであった。

• いわゆる三平方の定理である。
  　今日の教科書でも使われている図が
  　原論においても使われている。
  この証明は、
  　三角形の合同と
  　平行線による等積変形によっている。
  したがって、
  　原論第一巻の集大成といえる。
• この図において、
  　直線ＡＬ、ＢＫ、ＣＦが
  　一点において交わっている。
  これは、
  　相似比を考えると、
  　三平方の定理とチェバの定理を用いて証明できるが、
  　原論のこの段階では、証明できない。
• 命題1-47は、
  　△ＡＢＣ(_ＡＢ;;∠ＢＡＣ＝∠Ｒ)
  に対して、
  　正方(_ＢＣ)＝正方(_ＢＡ)＋正方(_ＡＣ)
  のことである。
  
• 命題1-47は推論用命題である。

  前提	作図	推論
  定義
  公準	1-1
  公理		1-1、1-2
  命題	1-31、1-46	1-4、1-14、1-41
  その他		コ2(題1-16)f

前 　　 次 　　 目次 　　頁頭