ユークリッド原論をどう読むか（６）
頁末 　　 前 　　 次 　　 目次　

ユークリッド原論

第３巻

命題３ー３（直径と弦）
もし
　円において
　中心を通る線分が
　中心を通らない弦を２等分するならば、
　それをまた直角に切る。
そしてもし
　直角に切るならば、
　それをまた２等分する。

• 円は定義１ー１５による。
• 中心は定義１ー１６による。
• 線分は定義の補足（命題１−１）による。
• 弦は定義３−４の補足による。
• 等分は定義の補足２（公理１ー６）による。
• 直角は定義１ー１０による。

ＡＢＣを円とし、
　それにおいて中心を通る線分ＣＤが
　中心を通らない弦ＡＢを
　点Ｆにおいて２等分するとせよ。

• 原論の立場からすれば、
  中心を通らない弦ＡＢが
  　あり、
  　ＡＢの２等分点をＦとする。
  中心Ｅが
  　命題３ー１（作図.円の中心）
  により、とられ、
  ＥとＦを通る直線が
  　公準１ー１（作図.直線）
  により、ひかれたとき、
  この直線は、
  　命題３ー１の補足(中心を通る直線は円周と２交点)
  により、
  　２点Ｃ、Ｄで円周と交わる
  　という作図の経過になる。
• 　円ＡＢＣ
  に対して、
  　弦ＡＢ.円ＡＢＣ、
  　中点Ｆ(ＡＢ)、
  　中心Ｅ.円ＡＢＣ、
  　交点Ｃ(直線ＥＦ,円ＡＢＣ;;同側(ＡＢ,Ｅ))、
  　交点Ｄ(直線ＥＦ,円ＡＢＣ;;反対側(ＡＢ,Ｅ))
  をとっている。

それをまた直角に切る《であろう
　と主張する》。




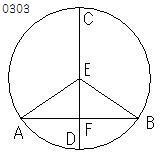
円ＡＢＣの中心がとられ、
　それをＥとし 【・・・(a)】

• 　前節のコメント参照のこと。
• 　中心Ｅ.円ＡＢＣ
  　Ｅ;点[ＣＤ]
  となっている。　

ＥＡ、ＥＢが結ばれたとせよ。

• 公準１ー１（作図.直線）
  による。
• 　線分ＥＡ、ＥＢ
  をとっている。

そうすれば
ＡＦは
　ＦＢに等しく、

• 命題の設定 による。
• 　ＡＦ＝ＦＢ
  となっている。

ＦＥは
　共通であるから、

• 命題の条件により、
  ＡＢは
  　中心を通らないので
  Ｅは、
  　ＡＢ上になく、
  　Ｆとは一致しないので
  線分ＥＦが存在し、
  　二つの三角形の合同について
  　論証が進められる。

２辺は
　２辺に等しい。 そして
　底辺ＥＡも
　底辺ＥＢに等しい。

• 定義１ー１５（円） による。
• 　(ＡＦ,ＦＥ)＝(ＢＦ,ＦＥ)、
  　ＥＡ＝ＥＢ
  をとっている。

それゆえ
角ＡＦＥは
　角ＢＦＥに等しい。

• 命題１ー８（３辺相等２）
  による。
• 　∠ＡＦＥ＝∠ＢＦＥ
  となっている。

ところが
　直線の上に直線が立てられて
　接角を互いに等しくするとき、
等しい角の双方は
　直角である。

• 定義１ー１０（直角）
  である。

ゆえに
　角ＡＦＥ、ＢＦＥの双方は
　直角である。

• 　前節による。
• 　∠ＡＦＥ＝∠ＢＦＥ＝∠Ｒ
  となっている。

したがって
中心を通るＣＤが
　中心を通らないＡＢを２等分するならば、
　それをまた直角に切る。
　
また
ＣＤが
　ＡＢを直角に切るとせよ。

• 　中心.円ＡＢＣ;点[線分ＣＤ]、
  　ＣＤ⊥ＡＢ
  となっている。

それをまた２等分する。
すなわち
ＡＦは
　ＦＢに等しいと主張する。
　
同じ作図がなされて、

• Ｅが、
  　命題３ー１（作図.円の中心）
  によって、とられることを述べている。
  　原論の立場からすると、
  中心を通らない弦ＡＢが
  　あり、
  中心Ｅが
  　命題３ー１（作図.円の中心）
  により、とられ、
  Ｅを通りＡＢに垂直な直線が
  　命題１ー１２（作図・線分への垂線）
  により、ひかれたとき、
  この直線は、
  　命題３ー１の補足(中心を通る直線は円周と２交点)
  により、
  　２点Ｃ、Ｄで円周と交わる
  　という作図の経過になる。
  結果的に同じ図になるが、
  　前半の作図とは経過がことなる。
  
• 　弦ＡＢ.円ＡＢＣ、
  　中心Ｅ.円ＡＢＣ、
  　交点Ｃ(垂線(Ｅ,ＡＢ),円ＡＢＣ;;同側(ＡＢ,Ｃ))、
  　交点Ｄ(垂線(Ｅ,ＡＢ),円ＡＢＣ;;反対側(ＡＢ,Ｃ))、
  　交点Ｆ(直径ＣＤ,ＡＢ)
  をとっている。

ＥＡは
　ＥＢに等しいから、

• (a) ,命題１ー８（３辺相等２）
  による。
  　ＥＡ＝ＥＢ
  となっている。

角ＥＡＦも
　角ＥＢＦに等しい。

• 命題１ー５（２等辺三角形の底角）
  による。
  
• 　∠ＥＡＦ＝∠ＥＢＦ
  となっている。

ところが
　直角ＡＦＥも
　直角ＢＦＥに等しい。

• 後半の命題の設定 による。
• ＥとＦが一致しないから、
  　ＡＦＥ、ＢＦＥが角をなす。
• 　∠ＡＦＥ＝∠ＢＦＥ＝∠Ｒ
  となっている。

それゆえ
ＥＡＦ、ＥＦＢは
　２角が２角に等しく、
　１辺が１辺に等しい、
すなわち
　等しい角の一つに対する辺ＥＦを共有する
　二つの三角形である。
ゆえに
　残りの辺も
　残りの辺に等しいであろう。

• 命題１ー２６（２角挟辺相等）
  である。
  なお、
  　命題１ー２６では、
  　等しい１辺が２角に挟まれていなくても
  　合同であることを主張している。
  ただ、
  　第３巻では、
  　平行線公準の成立を前提としているので、
  　三角形の和が２直角であることから、
  　２角挟辺相等の命題を論拠としても成立する。
• 　△ＥＡＦ≡△ＥＦＢ
  となっている。
  

したがって
ＡＦは
　ＦＢに等しい。

• 　前節による。
• 　ＡＦ＝ＦＢ
  となっている。

よってもし
　円において
　中心を通る線分が
　中心を通らない弦を２等分するならば、
　それをまた直角にきる。
そしてもし
　直角にきるならば、
　それをまた２等分する。
　
これが証明すべきことであった。

• 命題３ー３は、
  　円ＡＢＣ
  に対して、
  　弦ＡＢ.円ＡＢＣ、
  　中点Ｆ(ＡＢ)、
  　中心Ｅ.円ＡＢＣ、
  　交点Ｃ(直線ＥＦ,円ＡＢＣ;;同側(ＡＢ,Ｅ))、
  　交点Ｄ(直線ＥＦ,円ＡＢＣ;;反対側(ＡＢ,Ｅ))
  をとれば、
  　ＣＤ⊥ＡＢ、
  また、
  　弦ＡＢ.円ＡＢＣ、
  　中心Ｅ.円ＡＢＣ、
  　交点Ｃ(垂線(Ｅ,ＡＢ),円ＡＢＣ;;同側(ＡＢ,Ｃ))、
  　交点Ｄ(垂線(Ｅ,ＡＢ),円ＡＢＣ;;反対側(ＡＢ,Ｃ))、
  　交点Ｆ(直径ＣＤ,ＡＢ)
  をとれば、
  　Ｆ;中点(ＡＢ)
  のことである。
• 命題３ー３は推論用命題である。

  前提	作図	推論
  定義		1-10,1-15
  公準	1-1
  公理
  命題	1-12,3-1,3-1補	1-5,1-8,1-26
  その他

前 　　 次 　　 目次 　　頁頭