ユークリッド原論をどう読むか（６）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第３巻

命題３ー１７（作図.円外の点から円への接線）
与えられた点から
　与えられた円に
　接線をひくこと。
　

• 点は、定義１ー１による。
• 円は、定義１ー１５による。
• 接線は、定義３ー２の補足３による。

与えられた点をＡ、
　与えられた円をＢＣＤ
　とせよ。

• 　円ＢＣＤ、
  に対して
  　点Ａ[;;外.円ＢＣＤ]
  をとっている。

このとき
　点Ａから
　円ＢＣＤに
　接線を
　ひかなければならぬ。
　


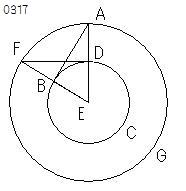
円の中心Ｅがとられ、【・・・(a)】

• 命題３ー１（作図.円の中心）
  による。
• 　中心Ｅ.円ＢＣＤ
  をとっている。

　ＡＥが結ばれ、

• 公準１ー１（作図.直線）
  による。
• 　線分ＡＥ
  をとっている。

　［ＡＥと円周ＢＣＤとの交点をＤとし、］

• 命題３−２の補足(円内通過直線は円周と２交点)
  により、
  　ＡＥは
  　円周と１点で交わる。
  この交点をＤとし、
  　溯ってＤを用いている。
• この記述がないと、
  　Ｄの位置が確定しない。
• 　交点Ｄ(ＡＥ,円ＢＣＤ)
  をとっている。

　Ｅを中心とし、
　ＥＡを半径として
　円ＡＦＧが描かれ、 【・・・(b)】

• 公準１ー３（作図.円）
  による。
• 　円ＡＦＧ(Ｅ,ＥＡ)
  をとっている。

　Ｄから
　ＥＡに直角に
　ＤＦがひかれ、 【・・・(c)】

• 命題１ー１１（作図・線分からの垂線）
  による。
• 　垂線ＤＦ'(Ｄ,ＥＡ)
  をとっている。

［上でひいた直線と
　その前に描いた円ＡＦＧの円周との
　交点をＦとする。］

• 点Ｄは
  　線分ＡＥ上の点であるから、
  　円ＡＦＧの内部の点である。
  命題３−２の補足(円内通過直線は円周と２交点)
  により、
  　Ｄから出る半直線は
  　円周ＡＦＧと１点で交わる。
  その点を改めてＦとし、
  　遡って用いている。
  
• この記述がないと、
  　Ｆの位置が確定しない。
• 　交点Ｆ(ＤＦ',円ＡＦＧ)
  をとっている。

　ＥＦ［が結ばれ、

• 公準１−１（作図.直線）
  による。
• 　線分ＥＦ
  をとっている。

　ＥＦと円周ＢＣＤとの交点をＢとし］、

• Ｅは円ＢＣＤの内部の点であり、
  　Ｆは外部の点であるから、
  　命題３−２の補足(円内通過直線は円周と２交点)
  により
  　１点で交わる。
  その点をＢとし、
  　遡って用いている。
• この記述がないと、
  　Ｂの位置が確定しない。
• 　交点Ｂ(ＥＦ,円ＢＣＤ)
  をとっている。

　ＡＢが結ばれたとせよ。

• 公準１−１（作図.直線）
  による。
• 　線分ＡＢ
  をとっている。

点Ａから
　円ＢＣＤに
　接線ＡＢがひかれた
　と主張する。

Ｅは
　円ＢＣＤ、ＡＦＧの
　　中心であるから、

• (a) ,(b) による。
• 　Ｅ;中心.(円ＢＣＤ、円ＡＦＧ)
  となっている。

ＥＡは
　ＥＦに、
ＥＤは
　ＥＢに
　等しい。

• 定義１−１５（円）
  による。
• 　ＥＡ＝ＥＦ、
  　ＥＤ＝ＥＢ
  となっている。

このとき
２辺ＡＥ、ＥＢは
　２辺ＦＥ、ＥＤに
　等しい。
そして
　Ｅにおける角を
　共通にはさむ。

• 　前節による。
• 　(ＡＥ、ＥＢ)＝(ＦＥ、ＥＤ)、
  　∠Ｅ;共通
  となっている。

それゆえ
底辺ＤＦは
　底辺ＡＢに
　等しく、
三角形ＤＥＦも
　三角形ＥＢＡに
　等しく、
残の角も
　残の角に
　等しい。

• 命題１−４（２辺挟角相等）
  による。
• 　△ＡＥＢ≡△ＦＥＤ
  となっている。

ゆえに
角ＥＤＦは
　角ＥＢＡに
　等しい。

• 　前節による。
• 　∠ＥＤＦ＝∠ＥＢＡ
  となっている。

ところが
角ＥＤＦは
　直角である。

• (c) による。
• 　∠ＥＤＦ＝∠Ｒ
  となっている。

したがって
角ＥＢＡも
　直角である。

• 公理１−１（同じものに等しい）
  による。
• 　∠ＥＢＡ＝∠Ｒ
  となっている。

そして
ＥＢは
　半径である。

• 定義１ー１６の補足（円の内部）
  による。
• 　ＥＢ;半径.円ＢＣＤ
  となっている。

円の直径に
　その端から
　直角にひかれた
　　直線は
　円に接する。
ゆえに
ＡＢは
　円《に》ＢＣＤ［に］接する。
　

• 定義１ー１７（直径）
  により、
  　ＥＢは直径の一部であり、
  　Ｂが直径の端である。
  命題３−１６の系（系．接線は直径と直角）
  による。
• 　ＡＢ（接）円ＢＣＤ
  となっている。

よって
　与えられた点Ａから
　与えられた円ＢＣＤに
　接線ＡＢがひかれた。
これが
　作図すべきものであった。
　

• 　命題３ー６の補足４(円外の点から引いた接線は２本)
  で
  　既に証明したことである。
• 命題３ー１７は、
  　円ＢＣＤ、
  に対して
  　点Ａ[;;外.円ＢＣＤ]、
  　中心Ｅ.円ＢＣＤ、
  　線分ＡＥ、
  　交点Ｄ(ＡＥ,円ＢＣＤ)、
  　円ＡＦＧ(Ｅ,ＥＡ)、
  　垂線ＤＦ'(Ｄ,ＥＡ)、
  　交点Ｆ(ＤＦ',円ＡＦＧ)、
  　線分ＥＦ、
  　交点Ｂ(ＥＦ,円ＢＣＤ)、
  　線分ＡＢ
  をとれば、
  　ＡＢ（接）円ＢＣＤ
  のことである。
  
• 命題３ー１７は作図用命題である。

  前提	作図	推論
  定義		1-15 ,1-16補 ,1-17
  公準	1-1 ,1-3
  公理		1-1
  命題	1-11 ,3-1 ,3-2補	1-4 ,3-16系
  その他

前 　　 次 　　 目次 　　頁頭